Description

Chalk 一直在和朋友们积极地环游世界，在最酷的地方拍照。最近，他来到了欧洲，研究了餐巾折叠的历史。从那以后，Chalk 就开始收集各种各样的餐巾来练习餐巾折叠艺术。

Chalk 的餐巾可以被定义为简单多边形。简单多边形是指没有边相交（除了相邻边在公共顶点处相交）的多边形。多边形的每个顶点都恰好属于两条边。

Chalk 折叠餐巾时，首先会在餐巾上画出折叠图案。折叠图案是一组 $\mathbf{K}-1$ 条线段，这些线段画在定义餐巾的多边形上。每条线段连接多边形边界上的两个有理数坐标点，并且完全位于多边形内部。折叠图案中的任意两条线段不能相交或重叠，除了可能在公共端点处。包含 $\mathbf{K}-1$ 条线段的折叠图案会将餐巾分成 $\mathbf{K}$ 个多边形区域。如果存在一条连续的路径（不一定是直线），连接两个点且不与多边形的任何边或折叠图案中的任何线段（即使是端点）相交，则这两个点属于同一区域。

Chalk 只对整齐的折叠图案感兴趣。折叠图案是整齐的，当且仅当与同一折叠线段 $F$ 相邻的任意两个区域关于 $F$ 对称。这意味着，如果沿着该线段折叠餐巾，这两个区域会完全重合。

下图展示了一个包含 $\mathbf{K}=8$ 个区域的整齐折叠图案。

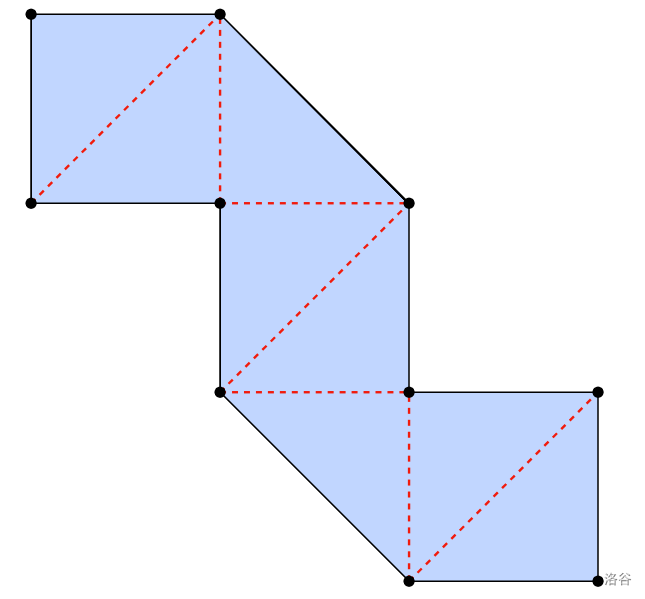
Chalk 已经用整齐的折叠图案成功折叠了他的大部分餐巾。但他收藏中还有一些餐巾，始终找不到整齐的折叠图案。对于这些餐巾中的每一块，Chalk 需要你的帮助，找出一个包含 $\mathbf{K}$ 个区域的整齐折叠图案，或者判断不存在这样的整齐折叠图案。

Input Format

输入的第一行包含测试用例数 $\mathbf{T}$。接下来是 $\mathbf{T}$ 组测试数据。每组测试数据的第一行包含两个整数 $\mathbf{N}$ 和 $\mathbf{K}$，分别表示定义 Chalk 餐巾的多边形的顶点数和需要用整齐折叠图案分割出的区域数（即折叠图案包含 $\mathbf{K}-1$ 条线段）。

定义餐巾的多边形用一组 $\mathbf{N}$ 个顶点表示，按顺时针方向沿多边形边界依次给出，起点任意。接下来的 $\mathbf{N}$ 行表示该顶点列表。第 $\mathbf{i}$ 行包含两个整数 $\mathbf{X}_{\mathbf{i}}$ 和 $\mathbf{Y}_{\mathbf{i}}$，表示第 $\mathbf{i}$ 个点在二维平面上的坐标为 $(\mathbf{X}_{\mathbf{i}}, \mathbf{Y}_{\mathbf{i}})$。

Output Format

对于每组测试数据，输出一行 Case #x: y，其中 $x$ 是测试用例编号（从 1 开始），$y$ 为 POSSIBLE 表示存在包含 $\mathbf{K}$ 个区域的整齐折叠图案，IMPOSSIBLE 表示不存在。

如果存在整齐折叠图案，将接着输出 $\mathbf{K}-1$ 行，每行表示一条折叠线段，顺序任意。每行格式为 $\mathbf{A}_{\mathbf{x}}$ $\mathbf{A}_{\mathbf{y}}$ $\mathbf{B}_{\mathbf{x}}$ $\mathbf{B}_{\mathbf{y}}$，其中 $(\mathbf{A}_{\mathbf{x}}, \mathbf{A}_{\mathbf{y}})$ 和 $(\mathbf{B}_{\mathbf{x}}, \mathbf{B}_{\mathbf{y}})$ 是线段的两个端点，顺序任意。$\mathbf{A}_{\mathbf{x}}$、$\mathbf{A}_{\mathbf{y}}$、$\mathbf{B}_{\mathbf{x}}$、$\mathbf{B}_{\mathbf{y}}$ 都应为 $\mathbf{N}/\mathbf{D}$ 的形式，其中 $\mathbf{N}$ 和 $\mathbf{D}$ 是正整数（无前导零），且互质，表示有理数 $\mathbf{N}/\mathbf{D}$。$\mathbf{N}$ 与 /、/ 与 $\mathbf{D}$ 之间不得有空格。

4
4 2
1 1
1 2
2 2
2 1
3 2
1 1
1 2
2 1
8 2
1 3
3 5
5 5
4 4
7 3
5 1
4 2
3 1
8 2
1 3
3 5
4 4
5 5
7 3
5 1
4 2
3 1

Case #1: POSSIBLE
1/1 2/1 2/1 1/1
Case #2: POSSIBLE
1/1 1/1 3/2 3/2
Case #3: IMPOSSIBLE
Case #4: POSSIBLE
1/1 3/1 7/1 3/1

1
10 8
4 1
3 1
2 2
2 3
1 3
1 4
2 4
3 3
3 2
4 2

Case #1: POSSIBLE
3/1 1/1 4/1 2/1
3/1 1/1 3/1 2/1
2/1 2/1 3/1 2/1
2/1 2/1 3/1 3/1
2/1 3/1 3/1 3/1
2/1 3/1 2/1 4/1
1/1 3/1 2/1 4/1

Hint

样例解释

注意：样例 2 不适用于测试集 1。只有样例 1 会在运行测试集 1 前被测试（与通常的样例测试方式一致）。此外，样例 2 不会在运行测试集 2 前被测试。

对于样例 1，$\mathbf{K}=2$ 时，可以用任意一条虚线画出整齐的折叠图案：

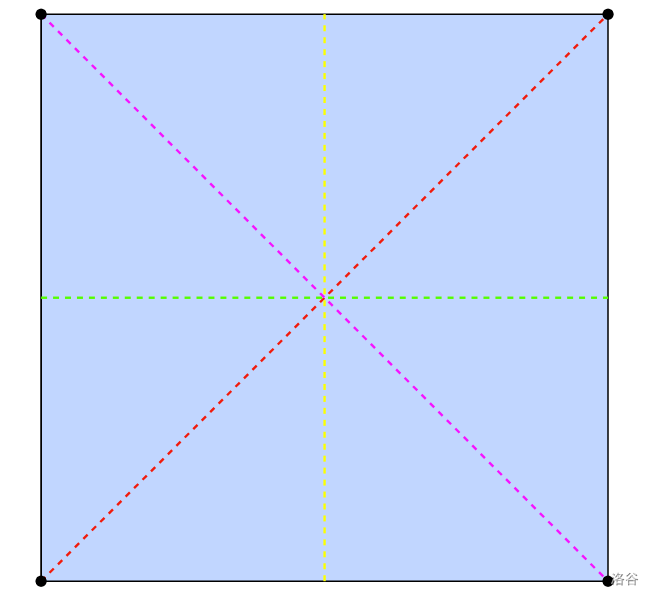
对于样例 2，$\mathbf{K}=2$ 时，可以如下画出整齐的折叠图案：

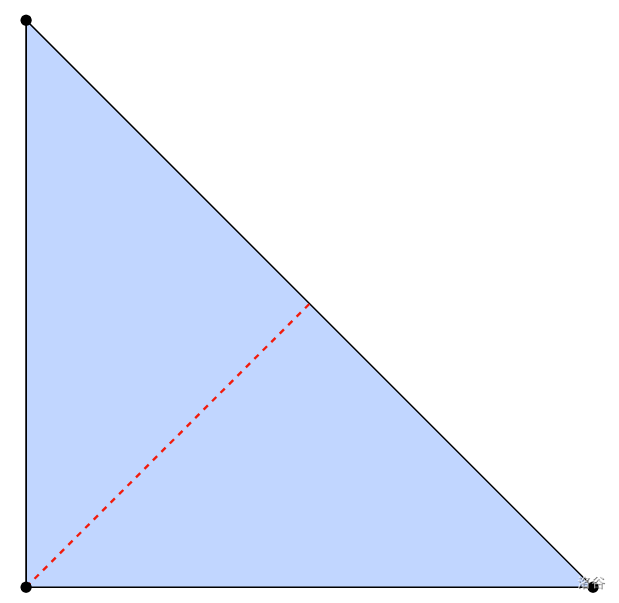
对于样例 3，没有整齐的折叠图案：

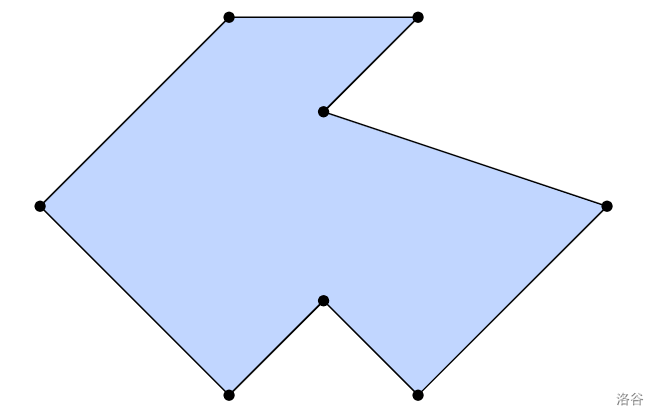
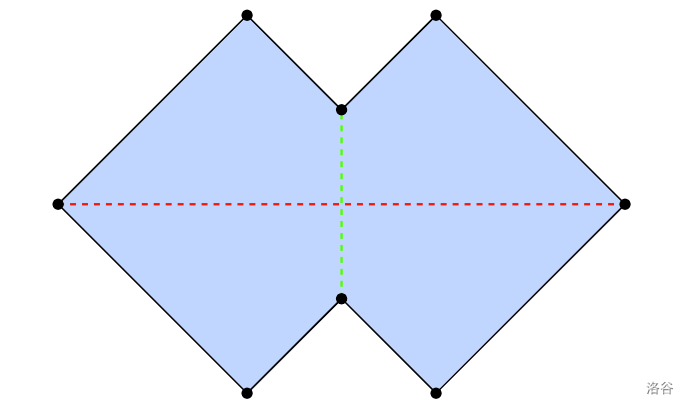
对于样例 4，存在两种可能的整齐折叠图案，$\mathbf{K}=2$：

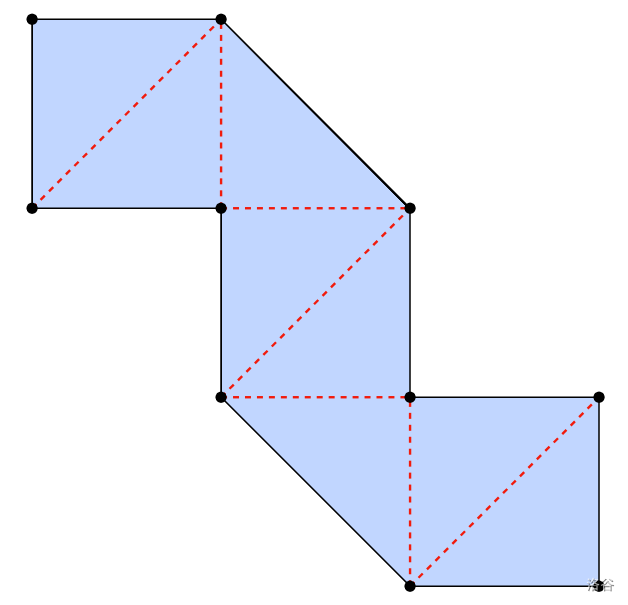
对于测试集 2 的样例，$\mathbf{K}=8$ 时，可以如下画出整齐的折叠图案：

数据范围

• $1 \leq \mathbf{T} \leq 100$。
• $3 \leq \mathbf{N} \leq 200$。
• $1 \leq \mathbf{X}_{\mathbf{i}} \leq 1000$，对所有 $\mathbf{i}$。
• $1 \leq \mathbf{Y}_{\mathbf{i}} \leq 1000$，对所有 $\mathbf{i}$。
• 所有 $\mathbf{N}$ 个点按顺时针顺序给出。
• 多边形任意两条相邻边不共线。
• 多边形为简单多边形，面积严格大于零。
• 除了相邻边在公共端点处外，多边形任意两条边不相交。

测试集 1（4 分，公开）

• $\mathbf{K}=2$。

测试集 2（39 分，隐藏）

• $2 \leq \mathbf{K} \leq 10$。

由 ChatGPT 4.1 翻译