Description

你被临时雇佣为围栏建设公司的员工，负责完成一块场地的围栏设计工作。每条围栏必须沿着直线连接两根立柱。每根立柱占据一个固定点，且任意三根立柱不共线。围栏之间不能相互交叉，但可以在端点（立柱位置）处相连。

前员工在项目中已经铺设了两条围栏后就离职了。现在需要由你来完成剩余设计。为了让老板和客户满意，你希望在不考虑围栏长度的情况下，尽可能多地添加围栏。

给定所有立柱的位置和已建好的两条围栏，请找出可以添加的最大数量的围栏，使得所有围栏（包括已有的和新增的）两两之间不交叉（仅在端点处相连是允许的）。

Input Format

输入的第一行包含测试用例数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 组测试用例：

1. 每组测试用例的第一行是一个整数 $\mathbf{N}$，表示立柱数量。
2. 接下来 $\mathbf{N}$ 行，每行包含两个整数 $\mathbf{X}_i$ 和 $\mathbf{Y}_i$，表示第 $i$ 根立柱的坐标。
3. 最后两行分别描述已有的两条围栏，每行包含两个整数 $\mathbf{P}_k$ 和 $\mathbf{Q}_k$，表示第 $k$ 条围栏连接第 $\mathbf{P}_k$ 根和第 $\mathbf{Q}_k$ 根立柱（立柱编号从 1 开始）。

Output Format

对于每组测试用例：

1. 首先输出一行 Case #x: y，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是能添加的围栏最大数量（不包括已有围栏）。
2. 接着输出 $y$ 行，每行包含两个不同的整数 $i$ 和 $j$（$1 \leq i, j \leq \mathbf{N}$），表示新增的围栏连接第 $i$ 根和第 $j$ 根立柱。
3. 所有围栏（包括已有的和新增的）必须满足两两不交叉（仅在端点处允许相连）。

2
4
0 0
0 1
1 1
1 0
1 2
3 4
5
0 0
0 1
1 1
1 0
2 3
1 2
3 5

Case #1: 3
1 4
2 3
4 2
Case #2: 6
5 4
2 4
5 2
1 4
4 3
3 2

Hint

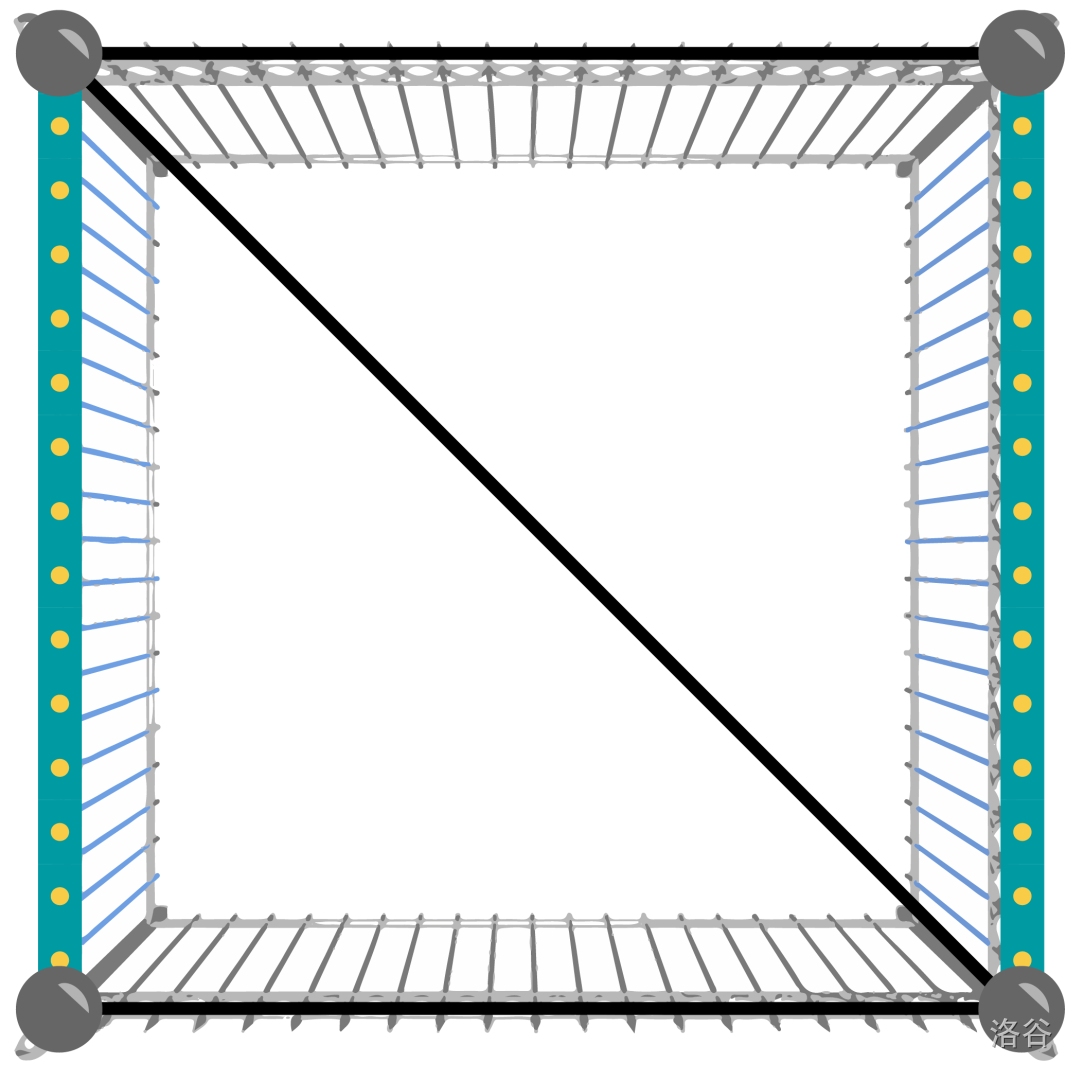
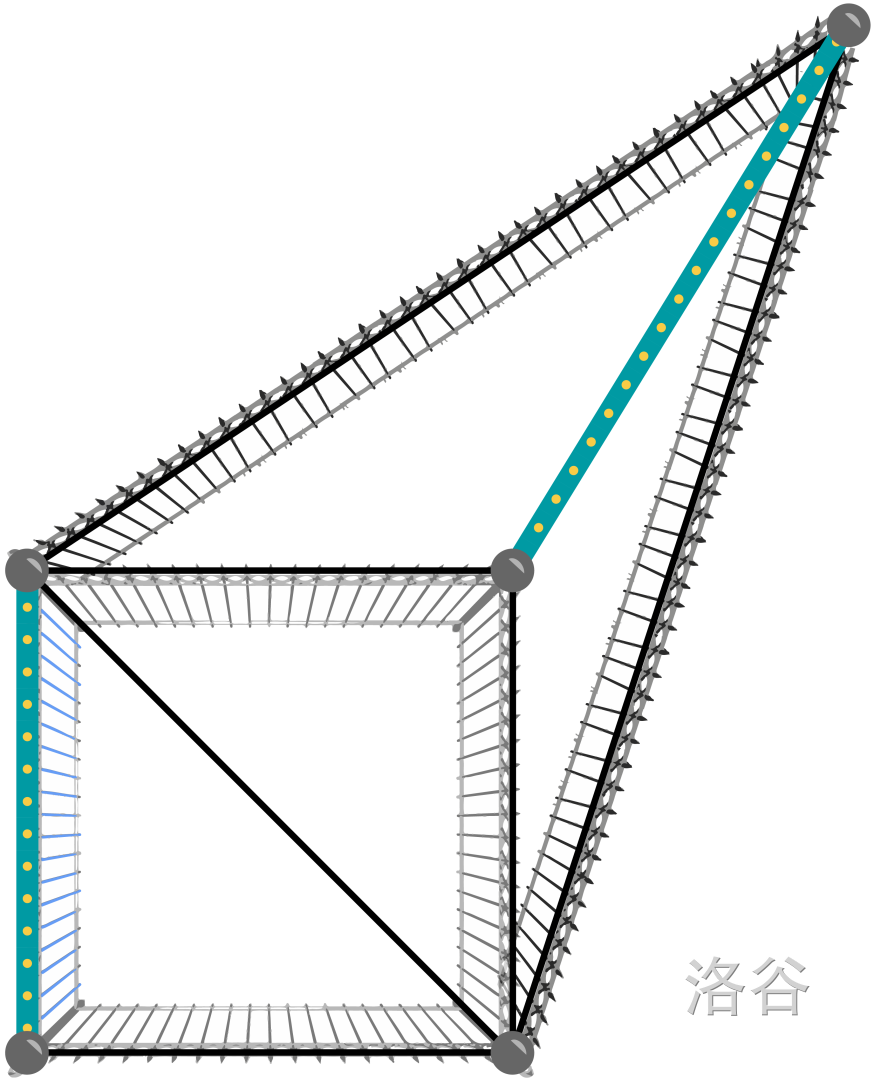
样例解释

下图展示了样例中的立柱和围栏布局。蓝色加粗线条表示已有围栏，其余线条表示样例输出中添加的围栏方案：

数据范围

• $1 \leq \mathbf{T} \leq 50$。
• 对所有 $i$，$-10^9 \leq \mathbf{X}_i, \mathbf{Y}_i \leq 10^9$。
• 对所有 $i \neq j$，$(\mathbf{X}_i, \mathbf{Y}_i) \neq (\mathbf{X}_j, \mathbf{Y}_j)$。
• 对所有 $k$，$1 \leq \mathbf{P}_k < \mathbf{Q}_k \leq \mathbf{N}$。
• 已有围栏之间不交叉（仅在端点处允许相连）。
• 任意三根立柱不共线。

测试集 1（11 分，可见判定）

• 时间限制：60 秒。
• $4 \leq \mathbf{N} \leq 100$。

测试集 2（19 分，隐藏判定）

• 时间限制：90 秒。
• $4 \leq \mathbf{N} \leq 10^5$。

翻译由 DeepSeek V3 完成