Description

Ueli 和 Vreni 正在玩一个游戏。游戏棋盘是一棵有 $\mathbf{N}$ 个顶点的树，初始所有顶点都是蓝色的。两人轮流操作，Ueli 先手。在每个回合中，玩家必须选择一个蓝色顶点及其任意数量（可以是零个或全部）的蓝色邻居顶点，并将这些顶点全部染红。如果在某个玩家的回合开始时所有顶点都是红色，则该玩家输掉游戏，另一方获胜。

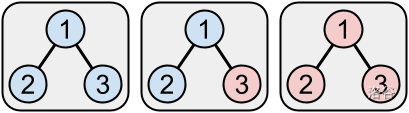
在下面的示例游戏中，Ueli 在第一回合将顶点 3 染红。然后，Vreni 选择顶点 2 并在她的回合中将其及其邻居（顶点 1）染红。由于所有顶点都已变红，Ueli 输掉游戏，Vreni 获胜。

Ueli 和 Vreni 注意到，由于 Ueli 先手，他更容易获胜。因此他们采用了以下规则：首先，Ueli 选择一个整数 $\mathbf{N}$；然后，Vreni 选择任意一棵有 $\mathbf{N}$ 个顶点的树；接着他们按照上述规则开始游戏，Ueli 先手。

Vreni 希望通过选择树的结构来克服后手的劣势。你能展示 Vreni 如何在这种设定下获胜吗？

交互协议

这是一个交互式问题。请确保你已阅读常见问题中关于交互式问题的部分。

开始时，你的程序应读取一个整数 $\mathbf{T}$，表示测试用例的数量。然后处理 $\mathbf{T}$ 个测试用例。

对于每个测试用例，你的程序首先读取一个整数 $\mathbf{N}$，表示 Ueli 选择的顶点数量。然后，你的程序需要输出 $\mathbf{N}-1$ 行来描述 Vreni 应选择的树结构。树的顶点编号为 1 到 $\mathbf{N}$。每行表示树的一条边，包含两个 1 到 $\mathbf{N}$ 的整数，表示该边连接的两个顶点。这些边必须构成一棵树。每行中的两个整数顺序不限，$\mathbf{N}-1$ 行的顺序也不限。

之后，你的程序需要读取一个整数 $\mathbf{M}$，表示需要在该树上进行的游戏数量。这些游戏是独立的，即每局游戏开始时所有顶点均为蓝色。

对于每局游戏，你需要处理若干轮交互，直到游戏结束。每轮交互包含双方各一个回合。

对于每轮交互，你的程序首先读取两行描述 Ueli 的回合。第一行是一个整数 $\mathbf{K}$，表示要染红的蓝色顶点数量。第二行包含 $\mathbf{K}$ 个互不相同的整数 $\mathbf{A}_1, \mathbf{A}_2, \ldots, \mathbf{A}_\mathbf{K}$，表示要染红的蓝色顶点。$\mathbf{K}$ 至少为 1，每个 $\mathbf{A}_i$ 在 1 到 $\mathbf{N}$ 之间。顶点 $\mathbf{A}_2, \mathbf{A}_3, \ldots, \mathbf{A}_\mathbf{K}$ 都必须是 $\mathbf{A}_1$ 的邻居。

然后，你的程序需要以相同格式输出 Vreni 的回合选择：第一行输出要染红的蓝色顶点数量，第二行输出这些顶点的编号，且除第一个顶点外，其他顶点都必须是第一个顶点的邻居。

如果 Vreni 的回合后所有顶点变红，则 Vreni 获胜，该局游戏结束。如果有下一局游戏，则立即开始；如果是该测试用例的最后一局游戏，则立即开始下一个测试用例（如果有）；如果是最后一个测试用例，评测机将不再发送输入，你的程序也不应再输出。

如果在 Ueli 的回合后所有顶点已变红，则 Vreni 输掉游戏，你的程序未通过该测试用例。此时，评测机会输出 -1 并不再处理后续输入，你的程序应适时退出。

如果评测机在任何时刻收到无效输入或输出（如格式错误、越界整数、非树结构的边、试图染红已为红色的顶点或不符合邻居条件的顶点），评测机也会输出 -1 并终止交互。若你的程序在收到 -1 后仍等待输入，将因超时而判为 Time Limit Exceeded。请注意，你有责任确保程序及时退出以避免超时错误。

评测机的行为是确定性的。即相同的输出会得到相同的输入。但同一棵树上的不同游戏可能会有不同操作。

Input Format

参见交互协议。

Output Format

参见交互协议。

2
3



1
1
3


4



2
3
2 1 3


2
2 3


-1

1 2
1 3



2
1 2

1 2
2 3
2 4



1
4


1
1

Hint

注意样例交互不满足任何测试集的约束（$\mathbf{N}$ 值过小），仅用于说明输入输出格式。

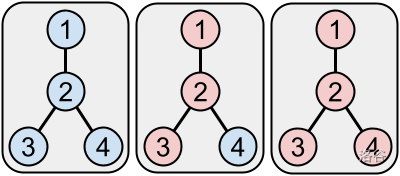
下图展示了测试用例 #2 中游戏 #1 的初始状态及每回合后的变化：

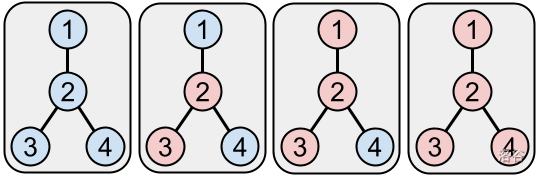
下图展示了测试用例 #2 中游戏 #2 的初始状态及每回合后的变化：

限制

• $1 \leq \mathbf{M} \leq 50$。

测试集 1（13 分，可见判题结果）

• $\mathbf{T}=1$。
• $\mathbf{N}=30$。

测试集 2（隐藏判题结果）

• $1 \leq \mathbf{T} \leq 10$。
• $31 \leq \mathbf{N} \leq 40$。
• 不同测试用例的 $\mathbf{N}$ 值互不相同。

翻译由 DeepSeek V3 完成