Description

由于调皮捣蛋，但丁被关进了一间由许多房间组成的奇怪房子。这栋房子是一个 $\mathbf{N} \times \mathbf{N}$ 的网格状房间布局，其中 $\mathbf{N}$ 为奇数且大于 1。左上角的房间编号为 1，其余房间按顺时针螺旋顺序依次编号为 $2, 3, \ldots, \mathbf{N}^{2}$。具体来说，编号从网格的顶行开始，每当遇到网格边界或已编号的房间时，向右转 90 度，最终到达网格正中央的房间。因为 $\mathbf{N}$ 是奇数，房子中心始终有一个房间，其编号恒为 $\mathbf{N}^{2}$。

例如，下图展示了 $\mathbf{N}=3$ 和 $\mathbf{N}=5$ 时的房间编号：

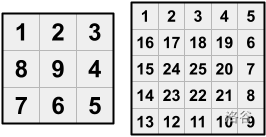
但丁从房间 1 出发，试图抵达中心房间（编号 $\mathbf{N}^{2}$）。在行进过程中，他只能从当前房间移动到编号更大且相邻的房间（两房间必须共享一条边，而非仅共享一个角落）。

但丁知道他可以按连续数字顺序移动——即若当前位于房间 $x$，则下一步移动到 $x+1$，依此类推。这样恰好需要 $\mathbf{N}^{2}-1$ 步。但他想按自己的方式行动！具体来说，他希望恰好用 $\mathbf{K}$ 步到达中心房间，其中 $\mathbf{K}$ 严格小于 $\mathbf{N}^{2}-1$。

为此，但丁需要通过一个或多个捷径实现。捷径是指两个非连续编号房间之间的移动。

以 $\mathbf{N}=5$ 的房屋为例：

• 若但丁位于 $1$，他不能移动到 $17$，但可移动到 $2$ 或 $16$。移动到 $2$ 不是捷径（因为 $1+1=2$），而移动到 $16$ 是捷径（因为 $1+1 \neq 16$）。
• 从 $2$ 可移动到 $3$（非捷径）或 $17$（捷径），但不能移动到 $1$、$16$ 或 $18$。
• 从 $24$ 只能移动到 $25$（非捷径）。
• 无法从房间 $25$ 移出。

更具体的例子：当 $\mathbf{N}=5$ 且 $\mathbf{K}=4$ 时，一种可行方案是 $1 \rightarrow 2 \rightarrow 17$（捷径）$\rightarrow 18 \rightarrow 25$（捷径）。如下图所示（红色箭头代表捷径）：

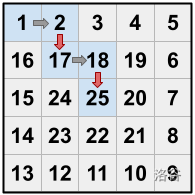
请你帮助但丁找到恰好 $\mathbf{K}$ 步到达中心房间的路径，或判断其不可能。

Input Format

第一行输入测试用例数量 $\mathbf{T}$。随后 $\mathbf{T}$ 行，每行包含两个整数 $\mathbf{N}$ 和 $\mathbf{K}$，分别表示房屋的维度（行列数）和但丁期望的移动步数。

Output Format

对于每个测试用例，输出一行 Case x: y，其中 $x$ 为用例编号（从 1 开始）。

若无法用恰好 $\mathbf{K}$ 步到达中心房间，$y$ 为 IMPOSSIBLE。

否则，$y$ 为但丁使用的捷径数量（因 $\mathbf{K} < \mathbf{N}^{2}-1$，至少需一次捷径）。随后输出 $y$ 行，每行两个整数 $a_i$ 和 $b_i$，表示第 $i$ 次捷径是从 $a_i$ 移动到 $b_i$（满足 $a_i+1 < b_i$）。

注意：这些行需按行进顺序排列，即对所有 $1 \leq i < y$ 有 $a_i < a_{i+1}$。

4
5 4
5 3
5 12
3 1

Case #1: 2
2 17
18 25
Case #2: IMPOSSIBLE
Case #3: 2
11 22
22 25
Case #4: IMPOSSIBLE

Hint

样例解释

样例 #1 对应题目描述中的示例。但丁的路径为 $1 \rightarrow 2 \rightarrow 17 \rightarrow 18 \rightarrow 25$。其中 $1 \rightarrow 2$ 和 $17 \rightarrow 18$ 是连续移动，故仅输出捷径 $(2 \rightarrow 17$ 和 $18 \rightarrow 25)$。

样例 #2 无解（注意但丁无法斜向移动）。

样例 #3 中，数字 $22$ 既是前一次捷径的终点，也是下一次的起点。输出中不能合并为 $11\ 22\ 25$，每行必须代表单独一次捷径。

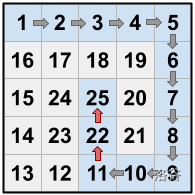
另一种仅需一次捷径的方案：$1 \rightarrow 2 \rightarrow \ldots \rightarrow 6 \rightarrow 19$（捷径）$\rightarrow 20 \rightarrow \ldots \rightarrow 25$。此方案同样有效，不要求最小化或最大化捷径次数。

样例 #4 中，但丁无法一步到达中心房间（此处为 $9$）。

数据范围

• $1 \leq \mathbf{T} \leq 100$。
• $1 \leq \mathbf{K} < \mathbf{N}^{2}-1$。
• $\mathbf{N} \bmod 2 \equiv 1$（$\mathbf{N}$ 为奇数）。

测试集 1（3 分，可见判定）

• 时间限制：5 秒。
• $3 \leq \mathbf{N} \leq 9$。

测试集 2（4 分，可见判定）

• 时间限制：20 秒。
• $3 \leq \mathbf{N} \leq 39$。

测试集 3（13 分，隐藏判定）

• 时间限制：20 秒。
• $3 \leq \mathbf{N} \leq 9999$。

翻译由 DeepSeek V3 完成