Description

坐标控制组织（Coordinate Control Organization）开发了一款自主机器人，用于在二维平面上巡逻 $N$ 个不同的重要地点。第 $i$ 个地点的坐标为 $(x_i, y_i)$，且保证任意三个地点不共线。

为了引导机器人巡逻，你可以在地面上绘制一些线段。每条线段必须直接连接两个重要地点，且任意两条线段不能相交（端点处除外）。

机器人将从任意一条线段的中点开始巡逻，初始朝向该线段的某一端点。它将按照以下规则无限移动：

• 只要机器人位于某条线段的内部，它就会向前移动，朝线段的一个端点前进。
• 当机器人到达一个重要地点时，它最初会背向刚刚经过的线段。机器人将向右（顺时针）旋转，直到视线与一条从当前地点出发的线段对齐，然后开始沿这条新线段移动。

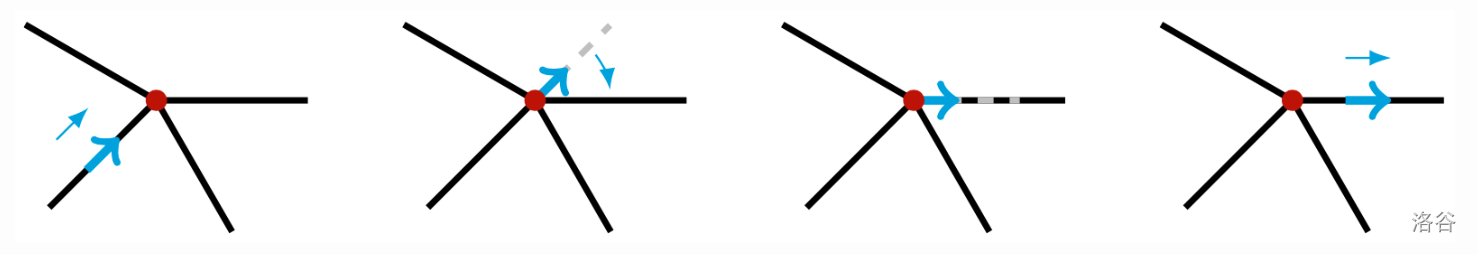
你的任务是绘制这些线段，使得无论机器人从何处开始，都能保证无限次访问每一个重要地点。可以证明这总是可行的。

Input Format

第一行输入一个整数 $N$（$2 \leq N \leq 2000$），表示重要地点的数量。

接下来的 $N$ 行每行包含两个以空格分隔的整数 $x_i$ 和 $y_i$（$-10^9 \leq x_i, y_i \leq 10^9$），表示第 $i$ 个重要地点的坐标。

保证所有 $N$ 个重要地点互不相同，且任意三点不共线。

Output Format

第一行输出一个正整数 $M$，表示你绘制的线段数量。

接下来的 $M$ 行每行包含两个以空格分隔的整数 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq N$，$u_i \neq v_i$），表示你在第 $u_i$ 个和第 $v_i$ 个重要地点之间绘制了一条线段。

如果有多种可行解，输出其中任意一种即可。

4
0 0
1 1
1 2
2 1

3
1 2
2 3
2 4

8
0 0
0 3
1 1
1 2
4 1
4 2
5 0
5 3

9
1 2
2 4
4 8
8 7
7 5
5 1
3 4
4 5
5 6

Hint

样例 1 解释

重要地点及绘制的线段如下图所示：

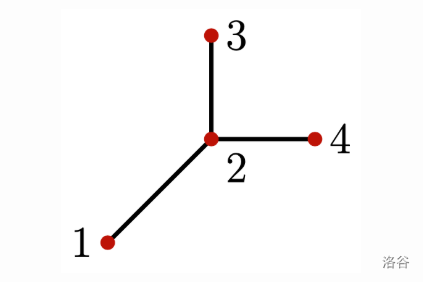
无论机器人从何处开始，它都会无限次访问每一个重要地点。例如，如果机器人从地点 $1$ 和 $2$ 之间的线段中点开始，朝向地点 $2$，则机器人访问地点的顺序为：

其中下划线部分无限循环。

样例 2 解释

重要地点及绘制的线段如下图所示：

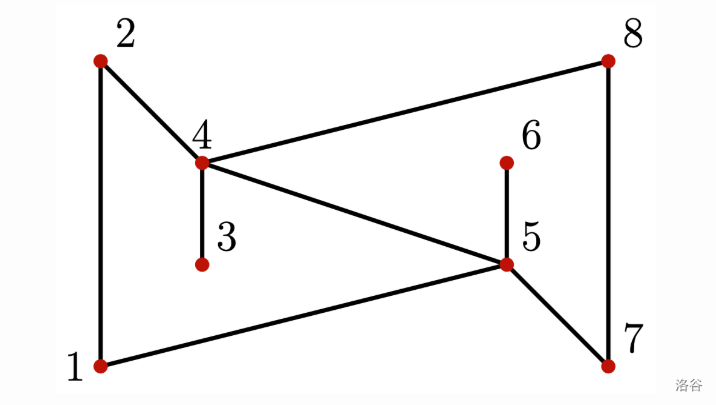
无论机器人从何处开始，它都会无限次访问每一个重要地点。例如，如果机器人从地点 $4$ 和 $5$ 之间的线段中点开始，朝向地点 $5$，则机器人访问地点的顺序为：

其中下划线部分无限循环。注意，并非所有线段都需要被无限次遍历，只要每个地点被无限次访问即可。

以下表格展示了 25 分的分布情况：

翻译由 DeepSeek V3 完成