Description

Onyaomale 正在领导一个项目，将高速公路沿线路灯的白炽灯泡更换为更节能且亮度更高的 LED 灯泡。她已将所有旧白炽灯泡拆除，现在专注于安装新的 LED 灯泡。由于新灯泡亮度更高，Onyaomale 认为部分路灯可能不再必要，通过停用这些路灯可以进一步节省能源。

我们将高速公路建模为一条从西向东延伸、长度为 $\mathbf{M}$ 米的直线。第 $x$ 米表示距离高速公路西端 $x$ 米的点。如果一盏路灯位于第 $x$ 米处，并安装了照明半径为 $\mathbf{R}$ 米的灯泡，则该路灯会照亮从第 $\max(0, x - \mathbf{R})$ 米到第 $\min(\mathbf{M}, x + \mathbf{R})$ 米（含端点）的高速公路段。Onyaomale 需要以最少数量的灯泡安装方案，确保高速公路的每个点都被至少一盏灯照亮。注意，这包括非整米距离的点。未安装灯泡的路灯不会照亮任何区域。

给定高速公路的长度 $\mathbf{M}$、新灯泡的照明半径 $\mathbf{R}$ 以及所有路灯的位置，求 Onyaomale 需要安装的最少灯泡数量以满足全路段照明需求。如果无法实现全路段照明，则报告不可能。

Input Format

输入的第一行包含测试用例数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例包含两行：第一行是三个整数 $\mathbf{M}$、$\mathbf{R}$ 和 $\mathbf{N}$，分别表示高速公路长度（米）、灯泡照明半径（米）和路灯数量；第二行包含 $\mathbf{N}$ 个按升序排列的整数 $\mathbf{X}_1, \mathbf{X}_2, \ldots, \mathbf{X}_\mathbf{N}$，表示路灯所在的位置（米）。

Output Format

对于每个测试用例，输出一行 Case #x: y，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为最少需要安装的灯泡数量。如果无法实现全路段照明，则 $y$ 为 IMPOSSIBLE。

3
10 3 3
2 7 9
10 2 3
2 7 9
10 2 4
2 3 7 9

Case #1: 2
Case #2: IMPOSSIBLE
Case #3: 4

Hint

样例解释

在样例 #1 中，Onyaomale 只需在最西侧和中间的路灯上安装灯泡，无需使用最东侧的灯。这两个灯泡分别覆盖 $[0,5]$ 和 $[4,10]$，因此整个高速公路 $[0,10]$ 均被照亮。

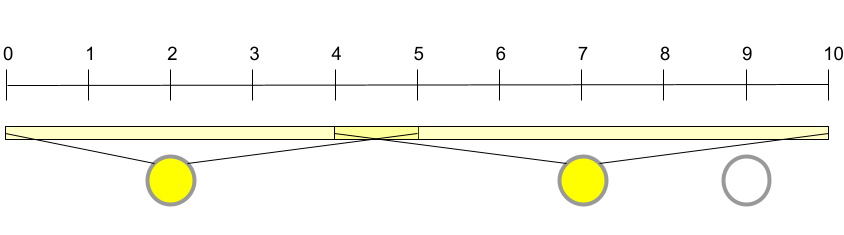
在样例 #2 中，配置与样例 #1 相同，但灯泡照明半径更小。此时无法实现全路段照明。即使所有路灯均点亮，第 $4$ 米与第 $5$ 米之间的中点仍未被覆盖。

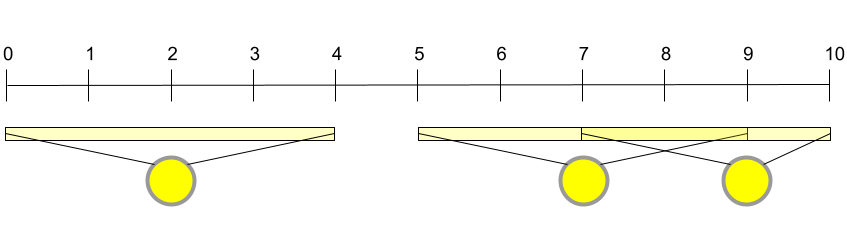
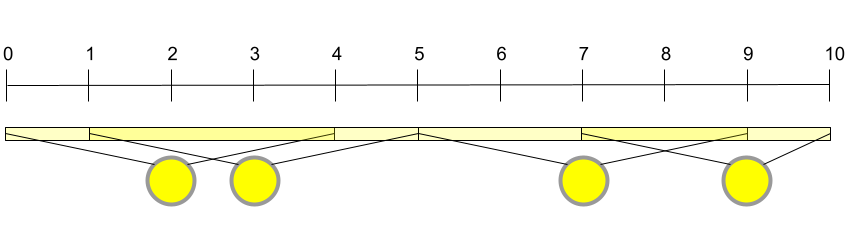
在样例 #3 中，相比样例 #2 新增了一盏位于第 $3$ 米的路灯。此时必须为所有路灯安装灯泡才能实现全路段照明。

数据范围

• $1 \leq \mathbf{T} \leq 100$。
• $1 \leq \mathbf{M} \leq 10^{9}$。
• $1 \leq \mathbf{R} \leq 10^{9}$。
• $0 \leq \mathbf{X}_{1}$。
• 对所有 $i$，满足 $\mathbf{X}_{i} < \mathbf{X}_{i+1}$。
• $\mathbf{X}_{\mathbf{N}} \leq \mathbf{M}$。

测试集 1（4 分，可见判定）

• $1 \leq \mathbf{N} \leq 10$。

测试集 2（10 分，可见判定）

• $1 \leq \mathbf{N} \leq 10^{5}$。

翻译由 DeepSeek V3 完成