Description

在往年的 NE(E)RC 竞赛中，曾多次出现关于仙人掌（cactus）的问题——这是一种连通无向图，其中每条边最多属于一个简单环。直观地说，仙人掌是树的推广，允许存在某些环。NEERC 2005 年题目中使用的传统仙人掌示例见样例部分的第二张图。

给定 $n$ 个整数 $d_1, d_2, \ldots, d_n$。请构造一个具有 $n$ 个顶点的仙人掌，使得顶点 $i$ 的度数为 $d_i$（即恰好有 $d_i$ 条相连的边），或者判定这样的仙人掌不存在。图中不允许出现平行边或自环。

Input Format

第一行包含一个整数 $n$（$2 \le n \le 2\,000$）——仙人掌的顶点数。

第二行包含 $n$ 个整数 $d_1, d_2, \ldots, d_n$（$1 \le d_i \le n-1$）——每个顶点期望的度数。

Output Format

如果无法构造满足条件的仙人掌，输出一个整数 $-1$。

否则，按照传统方式，将构造的仙人掌以边不重复的路径集合形式输出。

第一行输出一个整数 $m$——路径的数量。接下来的 $m$ 行，每行描述一条路径。路径应以一个整数 $k_i$（$k_i \ge 2$）开头，后跟 $k_i$ 个 $1$ 到 $n$ 的整数。这些整数表示路径中连续的顶点。路径中相邻顶点必须不同。路径可以多次访问同一顶点，但仙人掌的每条边在整个输出中必须恰好被遍历一次。

5
2 2 3 2 1

4
2 1 2
2 2 3
2 3 1
3 3 4 5

4
3 3 2 2

-1

6
1 2 1 1 2 1

-1

15
1 4 3 2 2 2 2 2 4 4 2 2 2 2 2

3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10

Hint

样例 1

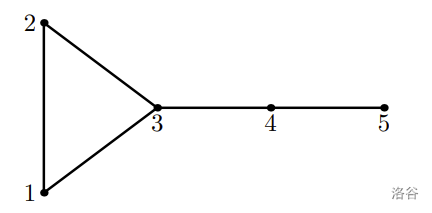
样例 4

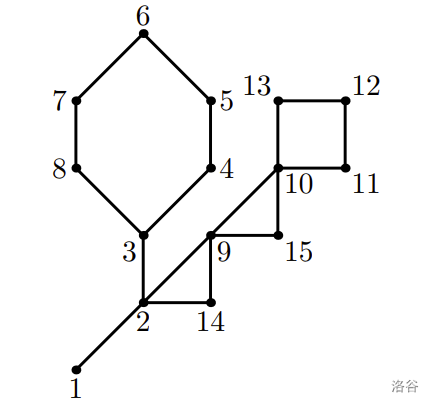
在第二个和第三个样例中，虽然存在满足给定度数的图，但它们都不是仙人掌。

翻译由 DeepSeek V3 完成