Description

给定数轴上的 $n$ 个线段 $[L_i; R_i]$。所有 $2n$ 个线段端点为两两不同的整数。

这些线段构成一个 层叠集——任意两条线段要么不相交，要么其中一条完全包含另一条。

请为每个线段选择一个非空子线段 $[l_i, r_i]$（要求 $L_i \le l_i < r_i \le R_i$ 且端点为整数），使得这些子线段互不相交（允许端点重合），并且它们的长度之和（$\sum_{i=1}^n r_i - l_i$）达到最大。

Input Format

第一行包含一个整数 $n$（$1 \le n \le 2 \cdot 10^3$）——线段数量。

接下来 $n$ 行，每行包含两个整数 $L_i$ 和 $R_i$（$0 \le L_i < R_i \le 10^9$）——第 $i$ 条线段的端点。

所有 $2n$ 个线段端点互不相同。给定的线段集合是层叠的。

Output Format

第一行输出子线段长度的最大可能和。

接下来的 $n$ 行，每行输出两个整数 $l_i$ 和 $r_i$（$L_i \le l_i < r_i \le R_i$），表示第 $i$ 条线段选择的子线段。

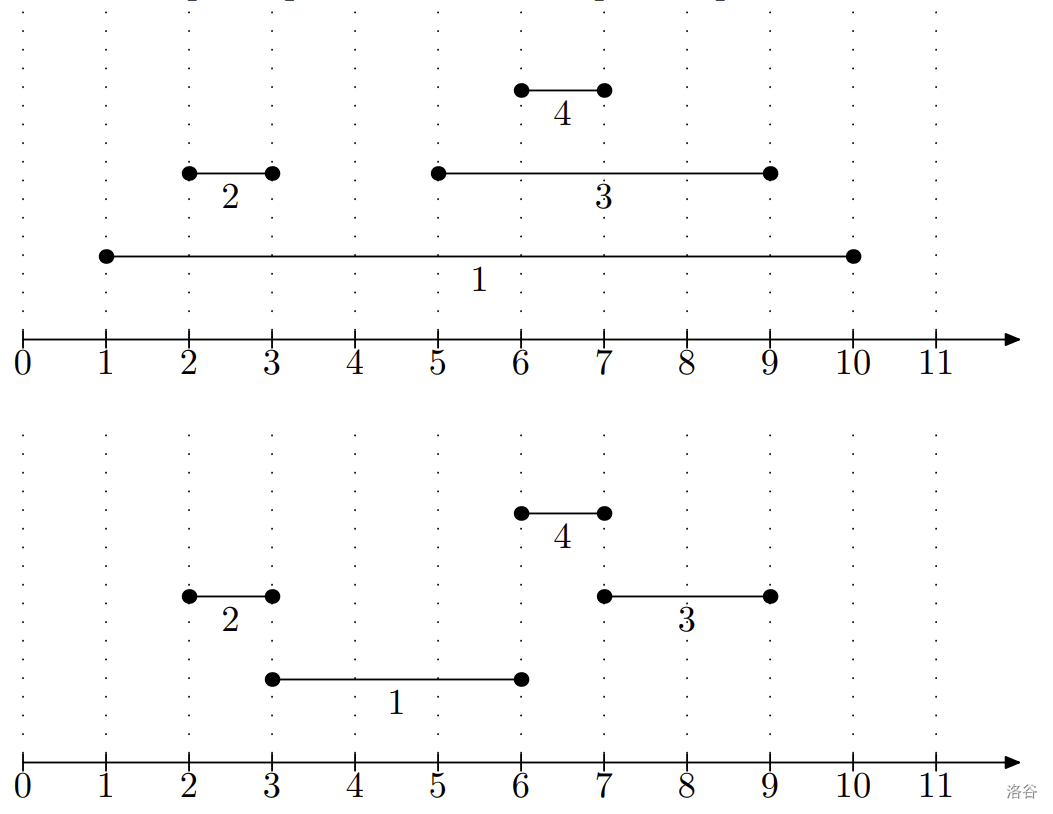
4
1 10
2 3
5 9
6 7

7
3 6
2 3
7 9
6 7

Hint

下图展示了示例输入和示例输出的对应关系。

翻译由 DeepSeek V3 完成