Description

Flato 住在平面国的首都 Flatburg，他刚刚买了一套新公寓！唯一的问题是，搬家工人把他最爱的沙发搬进来了，但放错了位置。现在 Flato 想通过移动沙发来解决这个问题，但这个沙发相当长。你能帮帮 Flato 吗？

和平面国的所有公寓一样，Flato 的公寓是一个凸多边形。他最喜欢的沙发无限薄，因此我们可以用一条线段来表示它。形式化地说，我们有一个表示公寓的多边形 $P$ 和一条位于多边形内部的线段 $AB$ 表示沙发。我们说沙发可以到达位置 $CD$，如果存在两个连续函数 $f$ 和 $g$ 从 $[0, 1]$ 映射到 $P$ 的内部或边界，满足 $f(0) = A$、$f(1) = C$、$g(0) = B$、$g(1) = D$，并且对于 $0 \leq x \leq 1$ 有 $|f(x)g(x)| = |AB|$。你的任务是找出在所有可到达的位置 $CD$ 中，直线 $AB$ 和 $CD$ 之间夹角的最大可能值。两条直线之间的夹角定义为它们在交点处两个角中的较小值，如果两条直线平行则定义为 $0$。

Input Format

输入的第一行包含五个整数 $n$、$x_A$、$y_A$、$x_B$ 和 $y_B$（$3 \leq n \leq 50$；$-15\,000 \leq x_A, y_A, x_B, y_B \leq 15\,000$）——多边形 $P$ 的顶点数以及沙发两端的坐标。

接下来的 $n$ 行每行包含两个整数 $x$ 和 $y$（$-15\,000 \leq x, y \leq 15\,000$）——按逆时针顺序给出的多边形顶点坐标。

保证 $A$ 和 $B$ 都在多边形 $P$ 的内部或边界上，且多边形是凸的。

Output Format

输出题目描述中所要求的最大角度（以度为单位）。如果你的输出的绝对误差或相对误差不超过 $10^{-6}$，则视为正确。

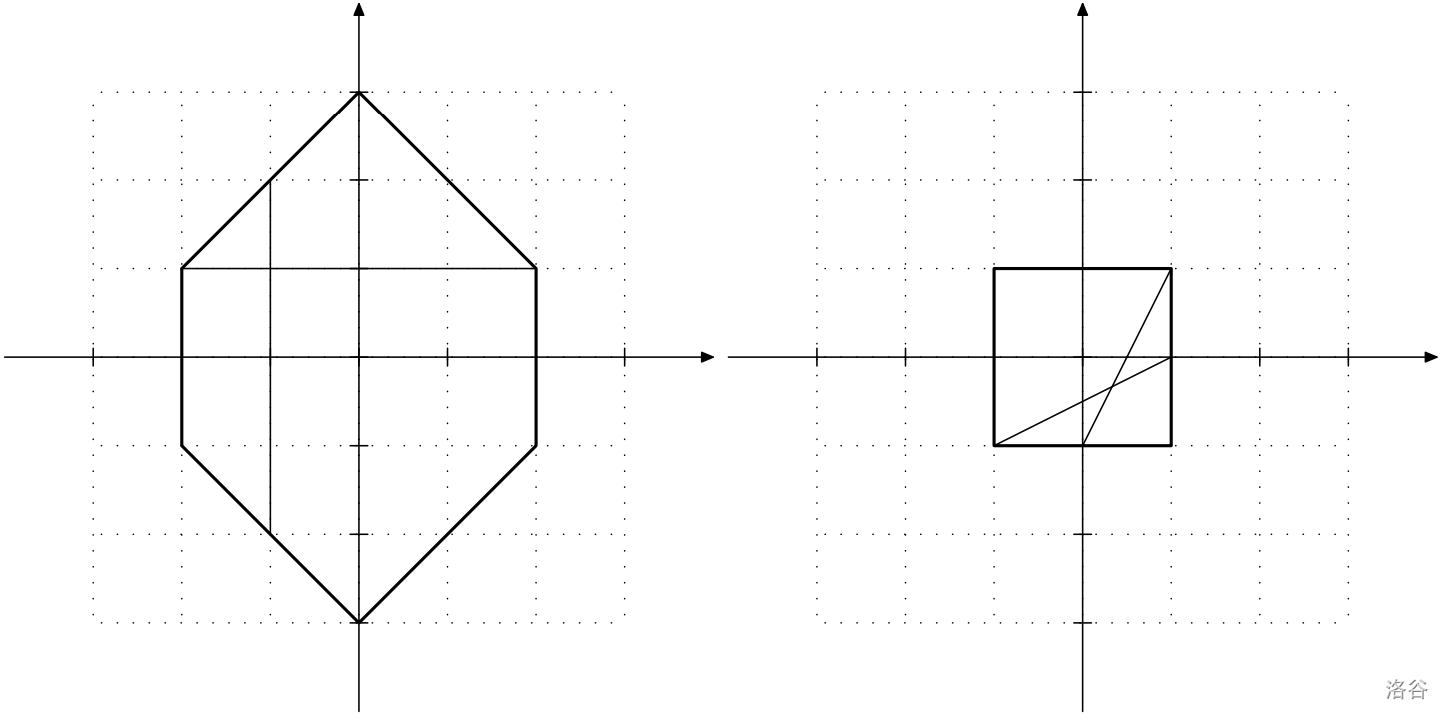
6 2 1 -2 1
2 1
0 3
-2 1
-2 -1
0 -3
2 -1

90

4 -1 -1 1 0
1 1
-1 1
-1 -1
1 -1

36.86989764584401285674

Hint

两条直线之间的夹角始终在 0 到 90 度之间。下方展示了两个样例的示意图，其中包含了初始位置和可能的最大角度对应的最终位置之一。

翻译由 DeepSeek V3 完成