Description

Julia 的 $n$ 个朋友想要在他们新搬去的国家创办一家初创公司。他们根据各自的工作内容（从前端到后端）给自己分配了编号 $1$ 到 $n$。他们还估计了一个矩阵 $c$，其中 $c_{ij} = c_{ji}$ 表示从事工作 $i$ 和 $j$ 的人之间每月的平均消息数量。

现在他们想要建立一棵层级树。这棵树将是一棵二叉树，每个节点包含团队中的一名成员。某位成员将被选为团队领导，并位于根节点。为了确保领导能够轻松联系到任何下属，对于树中的每个节点 $v$，必须满足以下条件：其左子树中的所有成员编号必须小于 $v$，而其右子树中的所有成员编号必须大于 $v$。

当层级树确定后，从事工作 $i$ 和 $j$ 的成员将通过他们在树中节点之间的最短路径进行通信。设该路径长度为 $d_{ij}$，则他们的通信成本为 $c_{ij} \cdot d_{ij}$。

你的任务是找到一棵层级树，使得所有成员对的通信总成本最小化：$\sum_{1 \le i < j \le n} c_{ij} \cdot d_{ij}$。

Input Format

第一行包含一个整数 $n$（$1 \le n \le 200$）—— 组织初创公司的团队成员数量。

接下来的 $n$ 行，每行包含 $n$ 个整数，第 $i$ 行的第 $j$ 个数是 $c_{ij}$ —— 团队成员 $i$ 和 $j$ 之间每月的估计消息数量（$0 \le c_{ij} \le 10^9$；$c_{ij} = c_{ji}$；$c_{ii} = 0$）。

Output Format

输出描述一棵最小化通信总成本的层级树。为此，对于编号从 $1$ 到 $n$ 的每个团队成员，输出其父节点的成员编号，如果是领导（根节点）则输出 $0$。如果存在多棵最优树，输出其中任意一棵的描述即可。

4
0 566 1 0
566 0 239 30
1 239 0 1
0 30 1 0

2 4 2 0

Hint

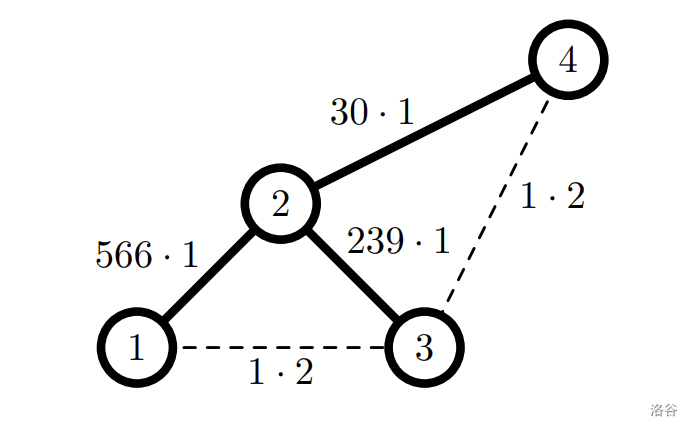
最小的可能总成本为 $566 \cdot 1 + 239 \cdot 1 + 30 \cdot 1 + 1 \cdot 2 + 1 \cdot 2 = 839$：

翻译由 DeepSeek V3 完成