Description

小 Fiona 有 $n$ 个大小各异的积木 $a_1, a_2, \ldots, a_n$，其中 $n$ 为偶数。有些积木的大小可能相同。她想把这些积木一块一块地堆叠起来，形成一个花式堆叠。

设 $b_1, b_2, \ldots, b_n$ 为从顶部到底部的积木大小序列。由于 Fiona 要使用所有积木，$b_1, b_2, \ldots, b_n$ 必须是 $a_1, a_2, \ldots, a_n$ 的一个排列。Fiona 认为堆叠是花式的，当且仅当满足以下两个条件：

1. 第二块积木严格大于第一块，之后每块积木交替严格小于或严格大于前一块。形式化地说，$b_1 < b_2 > b_3 < b_4 > \ldots > b_{n-1} < b_n$。
2. 位于偶数位置的积木大小严格递增。形式化地说，$b_2 < b_4 < b_6 < \ldots < b_n$（记住 $n$ 是偶数）。

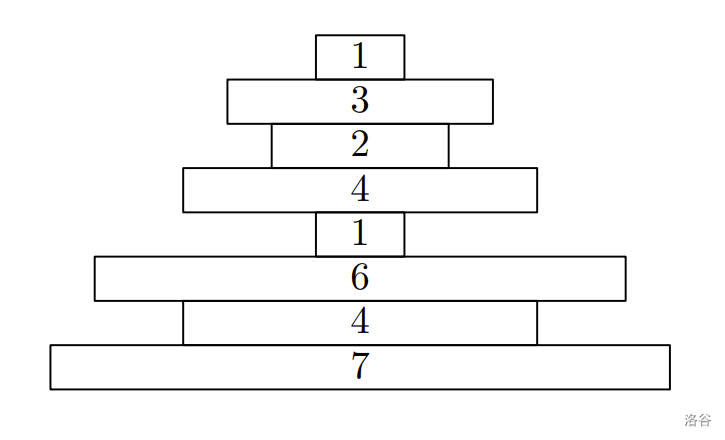
如果两个堆叠对应的序列 $b_1, b_2, \ldots, b_n$ 在至少一个位置上不同，则认为它们是不同的堆叠。

Fiona 想知道她能用所有积木堆出多少种不同的花式堆叠。由于大数字会让 Fiona 害怕，请将结果对 $998\,244\,353$ 取模后输出。

Input Format

每个输入包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 2500$）。接下来是每个测试用例的描述。

每个测试用例的第一行包含一个整数 $n$ —— Fiona 拥有的积木数量（$2 \le n \le 5000$；$n$ 为偶数）。第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$ —— 积木的大小，按非递减顺序给出（$1 \le a_1 \le a_2 \le \dotsb \le a_n \le n$）。

保证所有测试用例的 $n$ 之和不超过 $5000$。

Output Format

对于每个测试用例，输出可以构建的花式堆叠的数量，结果对 $998\,244\,353$ 取模。

2
4
1 2 3 4
8
1 1 2 3 4 4 6 7

2
4

Hint

翻译由 DeepSeek V3 完成