Description

一个地图是由符号集 $\{\texttt{U}, \texttt{L}, \texttt{D}, \texttt{R}\}$ 中的符号组成的矩阵。

地图矩阵 $a$ 的地图图集是一个有向图，包含 $n \cdot m$ 个顶点，编号为 $(i, j)$（$1 \le i \le n$；$1 \le j \le m$），其中 $n$ 是矩阵的行数，$m$ 是矩阵的列数。该图有 $n \cdot m$ 条有向边 $(i, j) \to (i + di_{a_{i, j}}, j + dj_{a_{i, j}})$，其中 $(di_U, dj_U) = (-1, 0)$；$(di_L, dj_L) = (0, -1)$；$(di_D, dj_D) = (1, 0)$；$(di_R, dj_R) = (0, 1)$。当地图图集中的所有边都指向图中的有效顶点时，该地图图集是有效的。

一个可容许地图是指其地图图集有效且由一组环构成的地图。

地图 $a$ 的描述是地图所有行的拼接——即字符串 $a_{1,1} a_{1,2} \ldots a_{1, m} a_{2, 1} \ldots a_{n, m}$。

给定一个字符串 $s$，你的任务是找出该字符串中有多少个子串可以构成某个可容许地图的描述。

字符串 $s_1s_2 \ldots s_l$ 的子串由一对索引 $p$ 和 $q$（$1 \le p \le q \le l$）定义，等于 $s_ps_{p+1} \ldots s_q$。当两个子串的索引对 $(p, q)$ 不同时，即使它们表示相同的字符串，也被认为是不同的子串。

Input Format

唯一的输入行包含一个字符串 $s$，由至少 1 个、最多 $20\,000$ 个符号 $\texttt{U}$、$\texttt{L}$、$\texttt{D}$ 或 $\texttt{R}$ 组成。

Output Format

输出一个整数——能够构成某个可容许地图描述的 $s$ 的子串数量。

RDUL

2

RDRU

0

RLRLRL

6

Hint

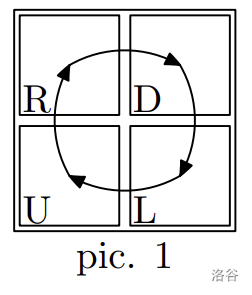
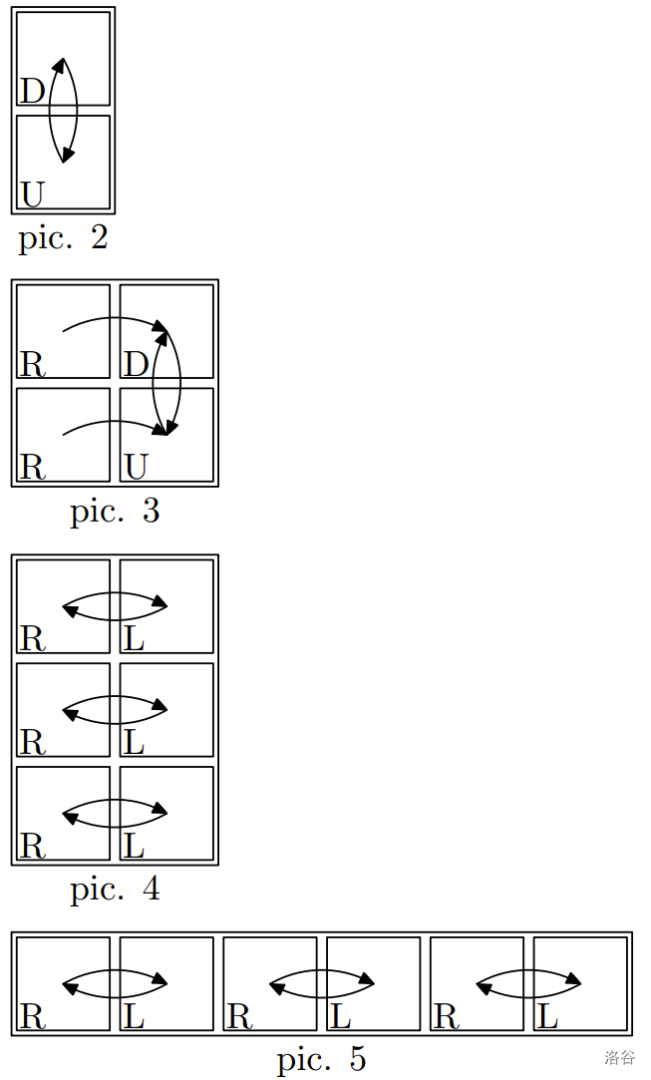
在第一个例子中，有两个子串可以构成可容许地图的描述——$\texttt{RDUL}$ 作为 $2 \times 2$ 的矩阵（图 1）和 $\texttt{DU}$ 作为 $2 \times 1$ 的矩阵（图 2）。

在第二个例子中，没有任何子串可以构成可容许地图的描述。例如，如果我们尝试将字符串 $\texttt{RDRU}$ 视为 $2 \times 2$ 的矩阵，可以发现生成的图不是一组环（图 3）。

在第三个例子中，三个子串 $\texttt{RL}$、两个子串 $\texttt{RLRL}$ 和一个子串 $\texttt{RLRLRL}$ 可以构成可容许地图，其中某些子串有多种方式。例如，子串 $\texttt{RLRLRL}$ 可以表示为 $3 \times 2$ 的矩阵（图 4）或 $1 \times 6$ 的矩阵（图 5）。

翻译由 DeepSeek V3 完成