Description

Alice 有一个漂亮的仙人掌图，她想把它画在一张纸上。Eve 威胁说要拿走这个仙人掌图的一个环，并沿着这个环上的所有边把纸剪开。这样一来，这张纸就会被分成两部分，Alice 会因此而难过。幸运的是，Barbara 刚刚给了 Alice 一个纸质环面——一张将顶边和底边、左边和右边分别连接起来且没有扭曲的纸。在环面上，有时你可以沿着一个环的所有边剪开纸，但它仍然会保持为一整块。请帮助 Alice 判断她是否能将她的仙人掌图画在一个环面上，使得 Eve 无法沿着任何一个环剪开纸并把环面分成两个不相连的部分。

仙人掌图 (Cactus) 是一个连通的无向图，其中每条边最多只属于一个简单环。直观地说，仙人掌图是树的一种推广，允许存在一些环。仙人掌图中不允许存在重边（一对顶点之间的多条边）和自环（连接一个顶点到其自身的边）。

我们说一个图被画在一张纸上，如果每个顶点是这张纸上的一个点，每条边是其对应顶点之间的线段，并且这些线段只在它们的端点处相交。在环面上，线段可以穿过纸的边界任意次数。

Input Format

输入包含一个或多个独立的测试用例。

每个测试用例的第一行包含两个整数 $n$ 和 $m$ ($1 \le n \le 10^5$; $0 \le m \le 10^5$)，其中 $n$ 是图中顶点的数量。顶点编号从 $1$ 到 $n$。图的边由一组边不重复的路径表示，其中 $m$ 是这些路径的数量。

接下来的 $m$ 行，每行描述了图中的一条路径。一条路径以一个整数 $s_i$ ($2 \le s_i \le 1000$) 开始，后面跟着 $s_i$ 个从 $1$ 到 $n$ 的整数。这 $s_i$ 个整数表示路径上的顶点。路径中相邻的顶点是不同的。路径可以多次经过同一个顶点，但在整个测试用例中，每条边都恰好被遍历一次。图中没有重边（任意两个顶点之间最多只有一条边）。

所有测试用例结束后的最后一行包含两个零。它不定义一个测试用例，仅仅是标记输入的结束，不需要任何输出。

输入中的所有图都是仙人掌图。在整个输入中，所有 $n$ 的值的总和以及所有 $m$ 的值的总和均不超过 $10^5$。

Output Format

对于每个测试用例，按照它们在输入中出现的顺序输出答案。对于每个测试用例，如果可以将这个仙人掌图画在环面上，则在单行中输出 Yes，否则输出 No。

6 1
8 1 2 3 1 4 5 6 4
10 2
9 1 2 3 1 10 4 5 6 4
5 7 8 9 7 10
0 0

Yes
No

Hint

将第一个样例中的仙人掌图画在环面上的一种方式如图片所示。

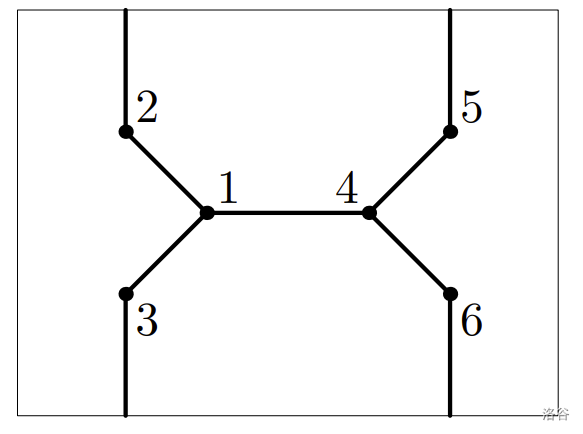
翻译由 gemini2.5pro 完成