Description

Pani Annochka 最近参加了一家 IT 公司的面试。在面试中，她被赋予了一个非常有趣的任务：

女孩被给定一个被划分为方格的区域。每个方格的边长为 $1$，且每个方格被涂成白色或黑色。

我们称一个棋盘区域的大小为 $n$ 和 $m$，当它由高度为 $n$ 个单位、宽度为 $m$ 个单位的矩形组成。此外，所有这些矩形必须被涂成白色或黑色，且每个白色矩形只能与黑色矩形相邻，反之亦然——每个黑色矩形只能与白色矩形相邻。

例如，以下棋盘的大小为 $2$ 和 $3$（蓝色为坐标轴）：

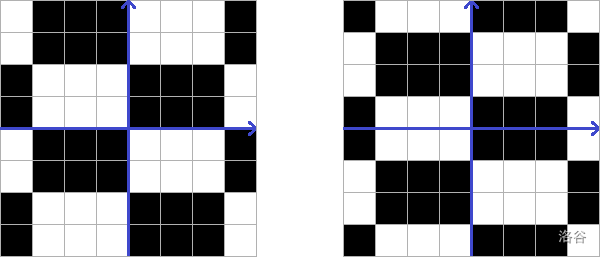
但以下这些不符合要求：

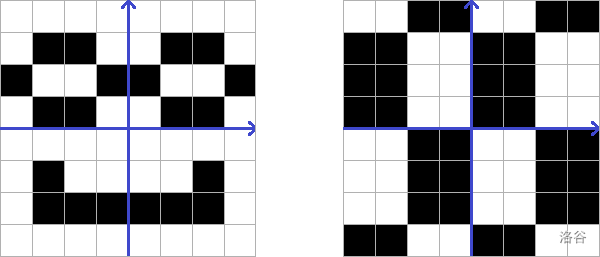
你可能已经注意到，大小为 $n$ 和 $m$ 的棋盘区域通常有很多种。挑战在于计算有多少种这样的棋盘区域。不不不，这太简单了。

Annochka 还知道该区域上的 $k$ 个方格及其颜色。Pani 需要找到满足以下条件的棋盘区域数量：这些方格在对应坐标处必须具有指定的颜色。帮助她完成这个任务！

更正式地说，给定 $k$ 组三元数：$x_i$, $y_i$, $c_i$，其中 $(x_i, y_i)$ 是方格左下角的坐标，$c_i$ 为 $0$ 表示该方格应为黑色，为 $1$ 表示该方格应为白色。你需要输出满足这些约束条件的大小为 $n$ 和 $m$ 的不同棋盘区域的数量。如果两个棋盘区域中至少有一个方格的颜色不同，则认为它们是不同的。

Input Format

第一行包含四个整数 $n$, $m$, $k$, $g$（$1 \leq k \leq 10^5$, $1 \leq n, m \leq 10^9$, $0 \leq g \leq 4$）——每个矩形的高度、每个矩形的宽度、已知方格的数量以及组别编号。

接下来的 $k$ 行，每行包含三个整数 $x_i$, $y_i$, $c_i$（$1 \leq x_i, y_i \leq 10^9$, $0 \leq c_i \leq 1$）——方格的坐标和颜色。注意，坐标可能重复。

Output Format

输出一个整数——满足给定约束条件的大小为 $n$ 和 $m$ 的不同棋盘区域的数量。

2 2 4 0
1 4 0
2 3 0
3 3 1
4 4 1

1

2 6 2 0
1 2 0
3 2 0

8

Hint

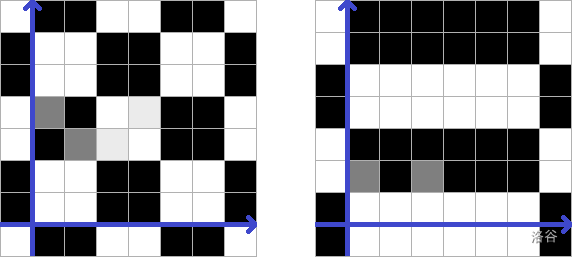
左侧是满足样例 $1$ 条件的唯一棋盘区域的示意图。

右侧是满足样例 $2$ 条件的 $8$ 种可能棋盘区域之一。

（蓝色为坐标轴，浅灰色表示应为白色的方格，深灰色表示应为黑色的方格）。

• （$17$ 分）：$1 \leq n, m, x_i, y_i, k \leq 100$；
• （$24$ 分）：$1 \leq n, m, k \leq 100$；
• （$31$ 分）：$1 \leq n \cdot m \leq 10^5$, $1 \leq k \leq 10^4$；
• （$28$ 分）：无额外限制。

翻译由 DeepSeek V3 完成