Description

一支足球队有 $n$ 名球员，编号为 $1$ 到 $n$ 的整数。编号为 $i$ 的球员的技能水平用整数 $c_i$ 描述。

球员们围成一个圆圈排列，编号为 $i$ 的球员右侧是编号为 $i+1$ 的球员（对于 $1 \le i < n$），而编号为 $n$ 的球员的下一个球员是编号为 $1$ 的球员。

我们定义一个游戏组合的强度，该组合由一个整数数组 $k=[k_0, k_1, k_2, \ldots, k_{m-1}]$ 描述，具体如下：

• 初始时，球在编号为 $1$ 的球员手中；
• 球员们无限轮流传球：在进行第 $i$ 次传球时，当前持球的球员会将球传给圆圈中右侧第 $x$ 个位置的球员，其中 $x=k_{((i-1) \mod m)}$；
• 游戏组合的强度定义为在上述过程中某个时刻持球的所有球员技能水平的最小值。

给定一个整数数组 $a_0, a_1, \ldots, a_{q-1}$。对于每个 $i$ 从 $0$ 到 $(q-1)$，求出由数组 $[a_0, a_1, \ldots, a_i]$ 描述的游戏组合的强度。

Input Format

第一行包含两个整数 $n$ 和 $q$ $(1 \leq n, q \leq 3 \cdot {10}^5)$ —— 球员数量和数组 $a$ 的长度。

第二行包含 $n$ 个整数 $c_1, c_2, \dots, c_n$ $(1 \leq c_i \leq n)$ —— 球员的技能水平。

第三行包含 $q$ 个整数 $a_0, a_1, \dots, a_{q-1}$ $(1 \leq a_i \leq n-1)$ —— 数组 $a$ 的元素。

Output Format

输出 $q$ 个整数 —— 所求的游戏组合的强度值。

6 3
6 3 5 4 2 1
3 1 2

4 1 2

Hint

在示例中，游戏组合的传球过程如下：

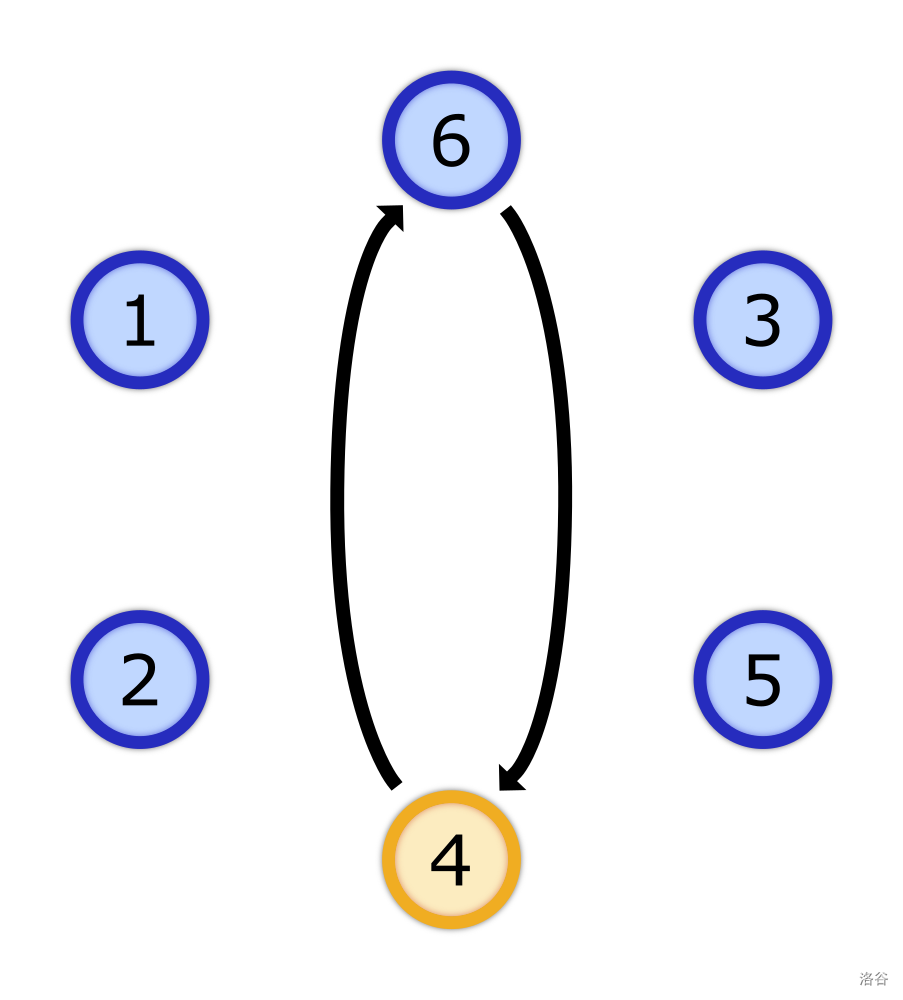
$k=[3]$

$k=[3,1]$

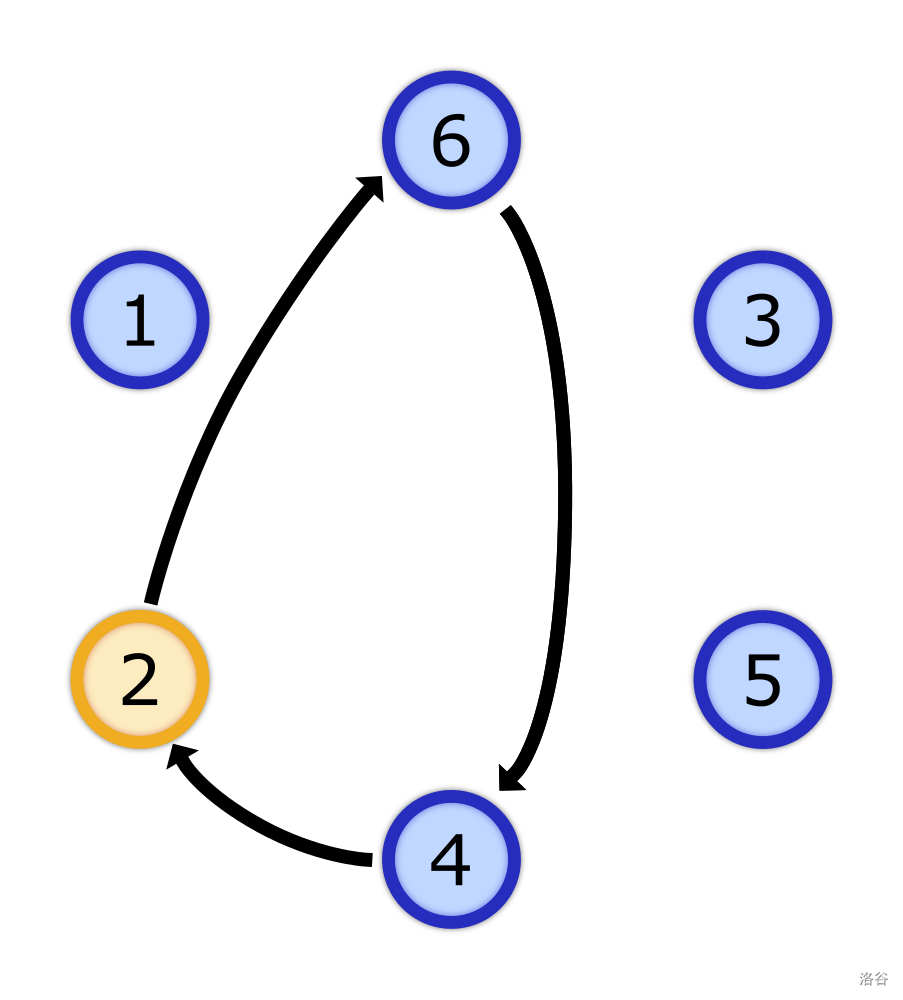
$k=[3,1,2]$

评分标准

• （$10$ 分）：$n, q \leq 100$；
• （$4$ 分）：所有 $a_i$ 的值相同；
• （$11$ 分）：$n$ 是一个质数；
• （$12$ 分）：$n, q \leq 1000$；
• （$16$ 分）：$n, q \leq 1.5 \cdot {10}^5$，且 $n = 2^k$（其中 $k$ 为某个整数）；
• （$25$ 分）：$n, q \leq {10}^5$；
• （$22$ 分）：无额外约束。

翻译由 DeepSeek V3 完成