Description

你被邀请协助一个参加"创新工坊"的学生团队——这是一个让学生团队发明并制作创新产品原型的活动。该团队开发了一款新型创新洗衣机，能显著降低洗衣所需的能耗。

这个创新点在于使用凸多边形而非圆形作为洗衣机滚筒的形状。现在给你这个多边形。滚筒以恒定速度绕多边形内部某个固定点旋转，每秒转 $1$ 圈。

目前原型机已经建成并开始测试。滚筒内有 $s$ 升水。在任何时刻，受重力影响的水都会占据滚筒底部面积为 $s$ 的区域。

位于水下的多边形顶点会受到压力。根据帕斯卡定律，压力与深度成正比。设在某一时刻有 $k$ 个顶点位于水下，其深度分别为 $d_1, d_2, \ldots, d_k$。我们定义压力失衡值为水下顶点深度与最大水下顶点深度的平均差值，即 $\frac{1}{k} \sum\limits_{i=1}^{k} \left(\max\limits_{j=1}^{k} d_j - d_i \right)$。注意 $d_i$ 的顺序不影响计算结果。

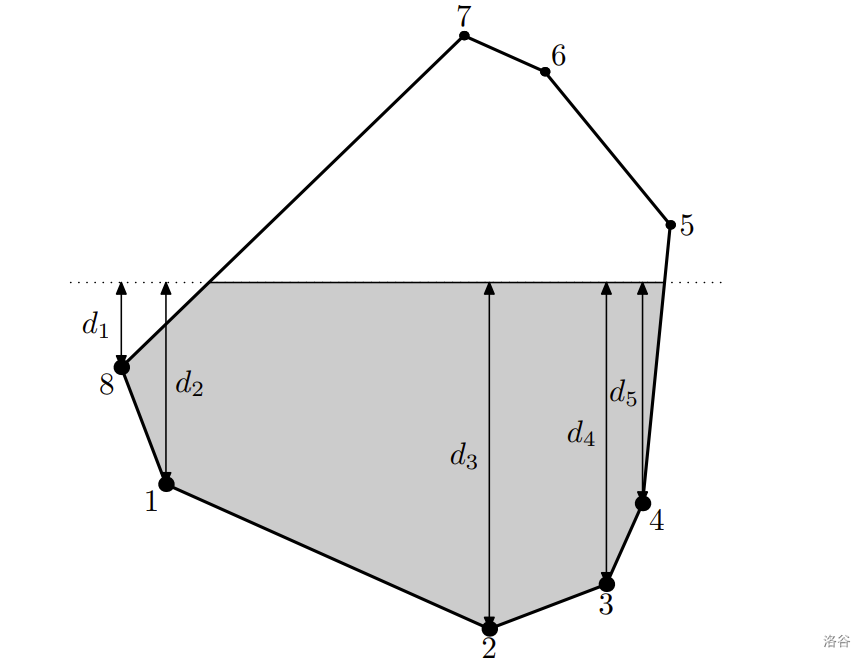
第三个测试用例中的多边形正在旋转。顶点 $1$、$2$、$3$、$4$、$8$ 位于水下。

为了选择最优的滚筒形状，团队需要知道在时间区间 $[0, 1]$（秒）内均匀随机选取时刻时压力失衡值的期望。请帮助团队计算这个值。

Input Format

第一行包含一个整数 $t$（$1 \leq t \leq 10^4$）——测试用例数量。接下来是各测试用例的描述。

每个测试用例的第一行包含两个整数 $n$, $s$（$3 \leq n \leq 2 \cdot 10^5$, $s \geq 1$）——多边形的顶点数和滚筒内的水量（升）。保证 $s$ 小于多边形面积。

接下来的 $n$ 行每行包含两个整数 $x_i$, $y_i$（$|x_i|, |y_i| \leq 10^8$）——多边形顶点的坐标。

保证给定点构成一个凸多边形。多边形面积为正且没有两条连续边共线。多边形顶点按逆时针顺序给出。

所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

Output Format

对于每个测试用例，输出一个实数——在随机均匀时刻的压力失衡值的期望。

当你的答案与标准答案的绝对误差或相对误差不超过 $10^{-5}$ 时视为正确。形式化地说，设你的答案为 $p$，标准答案为 $j$，则应满足：$\frac{|p - j|}{\max\{1, |j|\}} \le 10^{-5}$。

4
4 2
0 0
2 0
2 2
0 2
3 1
1 -1
0 1
-1 -1
8 18
-2 1
-2 -3
-1 -4
0 -4
3 -3
4 -1
4 0
-1 2
4 1
99999998 99999999
99999999 99999998
100000000 99999999
99999999 100000000

0.3729232286
0.1379212354
1.3663189952
0.2636965438