Description

F 城可以被表示为一棵树。一名著名逃犯正藏匿其中，今天一名忠实的警官决定不惜一切代价抓住他。警官比逃犯更强壮，但逃犯的速度远快于前者。因此追捕过程如下：在时刻 $t = 0$，警官出现在编号为 $s$ 的顶点，而逃犯可以选择任意其他顶点作为出生点。之后，他们轮流行动，警官先手。

• 警官的回合：她可以选择当前所在顶点的任意相邻顶点并移动过去。移动耗时 1 分钟。警官也可以选择停留在原地，此时她在当前顶点等待 1 分钟。如果在回合结束时警官与逃犯位于同一顶点，她会立即抓住逃犯，追捕结束。
• 逃犯的回合：设逃犯位于顶点 $b$，警官位于顶点 $p$。逃犯可以选择任意满足 $b' \ne p$ 且 $b$ 到 $b'$ 的路径不经过 $p$ 的顶点 $b'$，并瞬间移动过去。特别地，他可以选择 $b' = b$ 保持不动。逃犯的移动不消耗时间。

注意，逃犯一周前成功在警官的徽章上安装了无线电窃听器，因此逃犯始终知道警官的实时位置（包括初始顶点 $s$）。相反，警官对逃犯的移动一无所知，只有在抓住逃犯的瞬间才能发现他。

警官的目标是尽快抓住逃犯，而逃犯的目标是尽可能延迟被抓。由于追捕可视为不完全信息博弈，参与者可以采用混合（概率）策略——警官会最小化追捕的期望时长，逃犯会最大化该期望。

求在双方最优策略下追捕时长的数学期望。可以证明该期望总是有限的。特别地，在最优策略下，追捕无限持续的概率为零。

Input Format

第一行输入整数 $n$ 表示树的顶点数（$2 \le n \le 100$）。接下来 $n - 1$ 行描述 F 城的边：每行包含两个整数 $u_i$, $v_i$ 表示边的端点（$1 \le u_i, v_i \le n$），保证这些边构成一棵树。

最后一行输入整数 $s$ 表示警官的初始顶点编号（$1 \le s \le n$）。

Output Format

输出一个实数，表示最优策略下追捕时长的数学期望。若答案的绝对或相对误差不超过 $10^{-6}$ 则视为正确。形式化地，设你的答案为 $p$，标准答案为 $j$，需满足：$\frac{|p - j|}{\max\{1, |j|\}} \le 10^{-6}$。

2
1 2
2

1

3
1 2
1 3
1

2

4
4 3
4 1
4 2
4

3.66667

7
1 4
4 5
5 2
4 6
6 7
7 3
3

8.3525

Hint

样例中的树如下图所示。

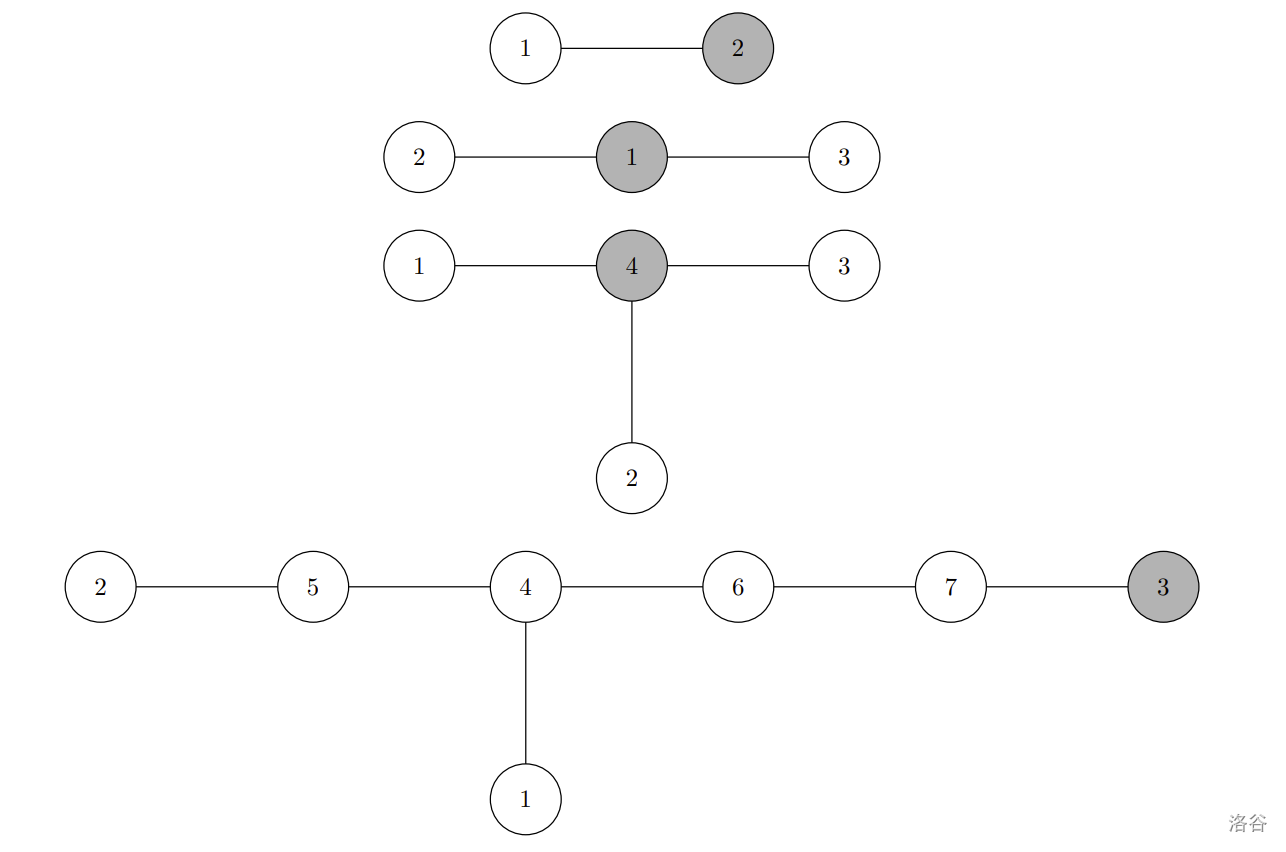
翻译由 DeepSeek V3 完成