Description

你负责在托伦郊区开发新的房产。你已经决定将建造一条主干道和沿街的 $n$ 处房产，编号从 1 到 $n$。该地区地势略有起伏，第 $i$ 处房产的海拔高度为 $a_i$ 厘米。

事实证明，没有人愿意购买位于斜坡上的房产。形式化地说，对于海拔高度序列 $a_1, a_2, \ldots, a_n$，一个斜坡是指满足以下条件的连续子序列 $a_{i-1}, a_i, \ldots, a_j, a_{j+1}$（其中 $2 \leq i \leq j \leq n-1$）：

1. $a_{i-1} < a_i = a_{i+1} = \ldots = a_j < a_{j+1}$，或者
2. $a_{i-1} > a_i = a_{i+1} = \ldots = a_j > a_{j+1}$。

直观地说，一个斜坡是指位置 $i-1, i, i+1, \ldots, j, j+1$ 上的连续房产区域，其中位置 $i, i+1, \ldots, j$ 的所有房产海拔高度都等于某个值 $h$，且 $h$ 严格位于 $a_{i-1}$ 和 $a_{j+1}$ 之间。

你可以任意增加或减少任何房产的海拔高度（以整数为单位调整），但当然你希望尽量减少总工作量。你的任务是确定消除所有斜坡所需的最小总海拔变化量。也就是说，你需要找到一组不存在斜坡的海拔高度 $b_1, b_2, \ldots, b_n$，使得 $|a_1 - b_1| + |a_2 - b_2| + \ldots + |a_n - b_n|$ 尽可能小。调整后的海拔高度 $b_i$ 必须是整数（特别地，它们不一定要是正数），且对 $b_i$ 没有其他约束。

Input Format

第一行包含一个整数 $n$（$1 \leq n \leq 2 \cdot 10^5$），表示沿街房产的数量。

第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$0 \leq a_i \leq 10^9$），其中第 $i$ 个整数 $a_i$ 表示第 $i$ 处房产的初始海拔高度。

Output Format

输出消除所有斜坡所需的最小总海拔变化量。

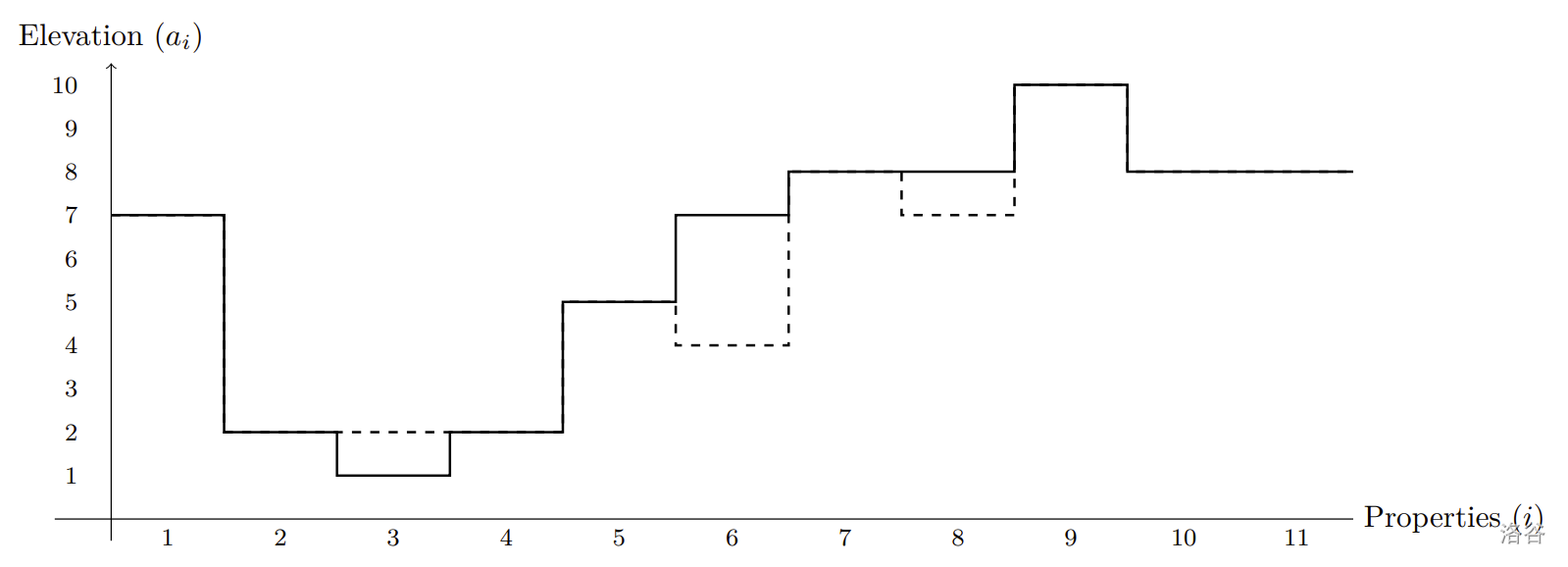
11
7 2 1 2 5 7 8 8 10 8 8

5

Hint

如下图所示。虚线表示调整后的无斜坡海拔高度 $b_i$ 与其对应房产的关系。

评分

翻译由 DeepSeek V3 完成