Description

Pavement 从 Gohcart 那里购买了一个激光玩具（Gohcart 原先是从 Rar the Cat 那里买的）。这个玩具有一个由 $h$ 行 $w$ 列组成的网格。网格的行编号从上到下为 $1$ 到 $h$，列编号从左到右为 $1$ 到 $w$。

每一行恰好包含一个上锁的滑动墙。初始时，第 $i$ 行的墙覆盖第 $l[i]$ 列到第 $r[i]$ 列（从 $1$ 开始编号），解锁它需要花费 $c[i]$ 美元。墙一旦解锁，就可以在第 $i$ 行上水平滑动到任意位置，只要它对齐在网格的边缘内即可。墙的任何部分都不能超出玩具的左边缘或右边缘。

每一列的顶部都有一个朝下的激光。如果某个滑动墙位于第 $i$ 列，那么它将阻挡第 $i$ 列上的激光。

一个可能的玩具示例如下，其中 $h = 3$，$w = 10$：

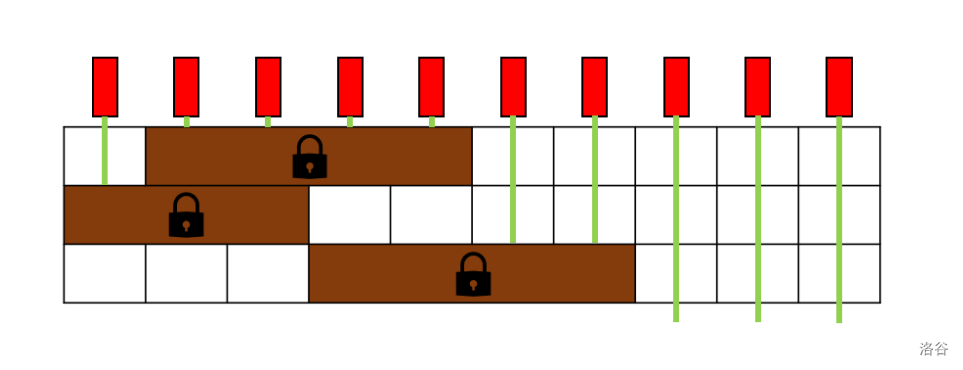
给定总预算 $k$ 美元，Pavement 的目标是在合理解锁并滑动墙壁的情况下，最大化未被阻挡的激光数量。请你确定他最多可以实现多少束未被阻挡的激光。

Input Format

你的程序必须从标准输入读取数据。

第一行输入包含三个用空格分隔的整数 $h, w$ 和 $k$，分别表示网格的行数、列数和预算。

接下来的 $h$ 行中，每行包含三个用空格分隔的整数，表示第 $i$ 行的滑动墙的信息，分别是 $l[i], r[i]$ 和 $c[i]$。

Output Format

你的程序必须将结果打印到标准输出。

输出一个整数，表示最多可以实现的未被阻挡的激光数量。

3 10 10
2 5 9
1 3 1
4 7 10

6

10 10 50
8 8 0
3 3 0
6 6 2
7 7 9
1 1 50
5 5 21
6 6 4
10 10 4
10 10 3
10 10 3

9

4 17 0
2 4 1000000000
6 9 1000000000
8 13 1000000000
15 16 1000000000

4

Hint

子任务

对于所有测试用例，输入将满足以下约束条件：

• $1 \leq h, w \leq 2000$
• $0 \leq k \leq 10^9$
• 对所有 $1 \leq i \leq h$，满足 $1 \leq l[i] \leq r[i] \leq w$
• 对所有 $1 \leq i \leq h$，满足 $0 \leq c[i] \leq 10^9$

你的程序将在满足以下特殊性质的输入数据上进行测试：

样例 1 解释

上图的激光玩具正对应该测试用例。Pavement 可以以 $9 + 1 = 10$ 美元的总价解锁第一个和第二个滑动墙。然后他可以将第一个滑动墙滑动到覆盖第 $4$ 到 $7$ 列，将第二个滑动墙滑动到覆盖第 $5$ 到 $7$ 列。

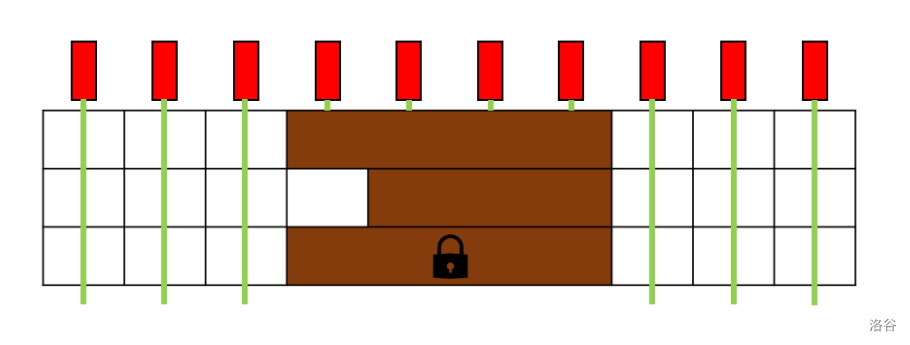
这样一来，$6$ 束激光（第 $1, 2, 3, 8, 9, 10$ 列）未被阻挡，这是能够实现的最大数量。

此样例适用于子任务 $3, 4, 5, 6, 8$。

样例 2 解释

此样例适用于子任务 $2$ 到 $8$。

样例 3 解释

此样例适用于子任务 $1, 3, 4, 5, 6, 8$。