Description

科学委员会计划访问 $n$ 个城市。这 $n$ 个城市通过恰好 $n - 1$ 条道路连接，使得可以使用这些道路在所有城市对之间移动。第 $i$ 条道路建在城市 $u[i]$ 和 $v[i]$ 之间。

每个城市都有自己的机场。为了开始旅程，委员会将从新加坡飞往其中一个城市。为了尽可能高效地利用旅程，委员会希望通过每条道路恰好两次（每个方向一次）来访问每个城市至少一次，然后从他们最终到达的城市飞回家。满足这个条件的旅程称为巡游。

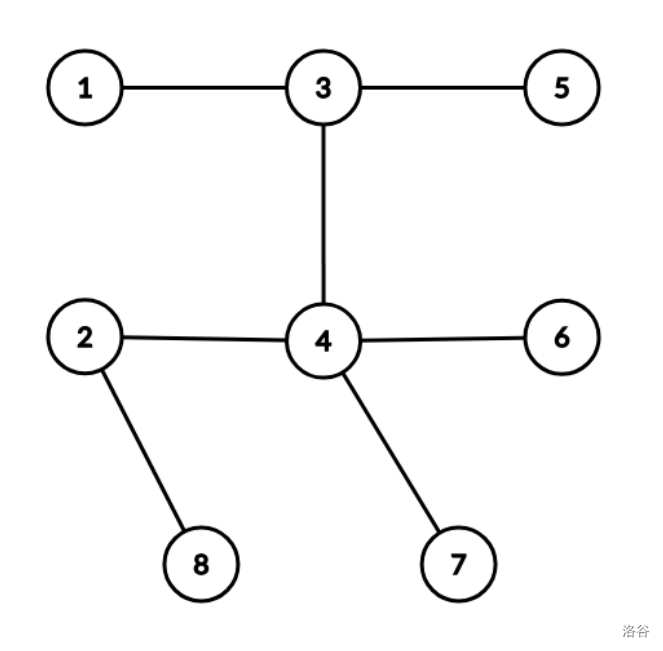
例如，设上图表示一个有 $n = 8$ 个城市的地图。从城市 $1$ 开始的一种可能的巡游是 $1 \to 3 \to 5 \to 3 \to 4 \to 2 \to 8 \to 2 \to 4 \to 6 \to 4 \to 7 \to 4 \to 3 \to 1$。注意这个巡游总共访问了所有城市 $2n - 1$ 次（等于 $15$），并且以起始城市（城市 $1$）结束。可以证明，对于所有可能的城市地图，所有巡游都满足这两个性质。

委员会还希望访问 $m$ 个按顺序从事件 $1$ 到事件 $m$ 发生的活动。事件 $j$ 将在城市 $s[j]$ 举行。一个城市可以举办零个、一个或多个活动，但不会有两个连续的活动在同一个城市举行，即 $s[j] = s[j + 1]$。

允许委员会访问所有活动的巡游必须按顺序访问城市 $s[1], s[2], \ldots, s[m]$，但不必连续。这样的巡游称为行程。形式上，设 $t[1], t[2], \ldots, t[2n - 1]$ 为某个巡游访问的城市序列。当且仅当 $s$ 是 $t$ 的一个子序列时，该巡游是一个行程。也就是说，可以通过删除 $t$ 中的零个或多个元素并保持剩下元素的顺序，得到 $s$。仍以上面的例子为例，假设 $m = 4$ 且 $s = [3, 5, 2, 7]$，那么巡游 $1 \to \textbf{3} \to \textbf{5} \to 3 \to 4 \to \textbf{2} \to 8 \to 2 \to 4 \to 6 \to 4 \to \textbf{7} \to 4 \to 3 \to 1$ 是一个行程，因为城市 $3, 5, 2, 7$ 按顺序在巡游中被访问（用粗体标记并下划线）。

委员会仍在决定从哪个城市出发，但他们同意：如果存在某个以该城市出发的行程，那么该城市就是一个好的出发选择。请帮助委员会判断对于所有城市，是否存在至少一个以该城市出发的行程。

Input Format

你的程序必须从标准输入读取数据。

输入的第一行包含两个用空格分隔的整数 $n$ 和 $m$，分别表示城市数量和事件数量。

接下来的 $n - 1$ 行中每行包含两个用空格分隔的整数。第 $i$ 行包含 $u[i]$ 和 $v[i]$，表示第 $i$ 条道路连接的两个城市。

最后一行输入包含 $m$ 个用空格分隔的整数 $s[1], s[2], \ldots, s[m]$，表示举办活动的城市。

Output Format

你的程序必须将结果打印到标准输出。

输出应包含 $n$ 行。如果存在以城市 $i$ 出发的行程，那么第 $i$ 行应包含一个整数 $1$。否则，输出一个整数 $0$。

8 4
1 3
2 4
3 4
4 6
5 3
2 8
7 4
3 5 2 7

1
0
1
1
0
1
1
0

8 4
1 3
2 4
3 4
4 6
5 3
2 8
7 4
3 2 5 7

0
0
0
0
0
0
0
0

4 7
1 2
1 3
1 4
2 1 2 1 2 1 2

0
0
0
0

5 2
1 2
2 3
3 4
4 5
2 4

1
1
1
1
1

Hint

子任务

对于所有测试用例，输入将满足以下约束条件：

• $2 \leq n \leq 200\,000$
• $1 \leq m \leq 2n - 1$
• $1 \leq u[i], v[i] \leq n$ 对所有 $1 \leq i \leq n - 1$
• $1 \leq s[j] \leq n$ 对所有 $1 \leq j \leq m$
• $s[j] \neq s[j + 1]$ 对所有 $1 \leq j \leq m - 1$
• 可以通过道路在所有城市对之间移动。

你的程序将在满足以下特殊性质的输入数据上进行测试：

样例 1 解释

此样例适用于子任务 $5, 6, 7, 9$。

这个样例在题目中已经作为示例说明。

存在以城市 $1, 3, 4, 6$ 和 $7$ 开始的行程。在题目中已给出一个以城市 $1$ 开始的行程。

另一方面，可以证明城市 $2, 5$ 和 $8$ 没有任何行程可以以它们为起点。

样例 2 解释

此样例适用于子任务 $5, 6, 7, 9$。

这个测试用例与题目示例相同，除了 $s[2]$ 和 $s[3]$ 被交换了。此时不存在任何行程。

样例 3 解释

此样例适用于子任务 $1, 2, 5, 6, 7, 8, 9$。

样例 4 解释

此样例适用于子任务 $3, 4, 5, 6, 7, 9$。