Description

在一个非常古老的操作系统中，屏保由两个在屏幕上飞来飞去的矩形组成。屏幕宽 $W$ 像素，高 $H$ 像素。我们规定屏幕左上角为坐标原点，$x$ 轴从原点向右延伸，$y$ 轴从原点向下延伸。

第 $i$ 个矩形（$i=1,2$）的宽度为 $w_i$ 像素，高度为 $h_i$ 像素，初始时其左上角坐标为 $(x_i, y_i)$，初始移动方向为 $(\delta x_i, \delta y_i)$，其中 $\delta x_i$ 和 $\delta y_i$ 的取值均为 $-1$ 或 $1$。每过一秒，矩形 $i$ 的左上角坐标都会立刻变化 $(\delta x_i, \delta y_i)$。

每当矩形 $i$ 碰到屏幕的左边界或右边界时，$\delta x_i$ 的符号会在下一秒之前反转。同样地，每当矩形 $i$ 碰到屏幕的上边界或下边界时，$\delta y_i$ 的符号会在下一秒之前反转。如果矩形 $i$ 同时碰到两条边界（只能发生在屏幕的角落处），那么 $\delta x_i$ 和 $\delta y_i$ 都会反转。

因此，两个矩形始终完全位于屏幕内部。简而言之，矩形与屏幕边界的碰撞是完全弹性的。注意，尽管如此，矩形的移动依然是离散的：每过一秒，矩形的坐标瞬间移动 $1$ 个像素单位。

你很好奇这两个矩形有多频繁地重叠。当两个矩形的交集面积为正时，认为它们发生了重叠。

设 $f(t)$ 表示在第 $0, 1, \ldots, t-1$ 秒内，矩形发生重叠的时刻数量（其中第 $0$ 秒是矩形开始移动之前）。

请你求出 $\dfrac{f(t)}{t}$ 在 $t \to +\infty$ 时的极限，并以最简分数的形式表示。可以证明，该极限值是一个有理数。

Input Format

每个测试包含多个测试用例。

第一行包含一个整数 $T\;(1 \le T \le 1000)$，表示测试用例的数量。

接下来是每个测试用例的描述。

每个测试用例的第一行包含两个整数 $W$ 和 $H$，表示屏幕的宽和高（$3 \le W,H \le 4000$）。

接下来的两行分别描述两个矩形。每个矩形由六个整数 $w_i, h_i, x_i, y_i, \delta x_i, \delta y_i$ 描述，表示第 $i$ 个矩形的宽度、高度、左上角坐标以及初始移动方向（$1 \le w_i \le W-2$；$1 \le h_i \le H-2$；$0 < x_i < W-w_i$；$0 < y_i < H-h_i$；$\delta x_i, \delta y_i \in \{-1, 1\}$）。

保证所有测试用例中 $W+H$ 的总和不超过 $8000$。

Output Format

对于每个测试用例，输出一行，包含两个用斜杠（$\tt{/}$）分隔的整数 $p$ 和 $q$（中间无空格），表示 $\dfrac{f(t)}{t}$ 的极限值为 $\dfrac{p}{q}$。输出的分数必须是最简形式，即 $p$ 和 $q$ 的最大公约数为 $1$。

2
3 3
1 1 1 1 1 1
1 1 1 1 1 -1
5 4
2 2 1 1 -1 -1
2 1 2 2 1 -1

1/2
1/3

Hint

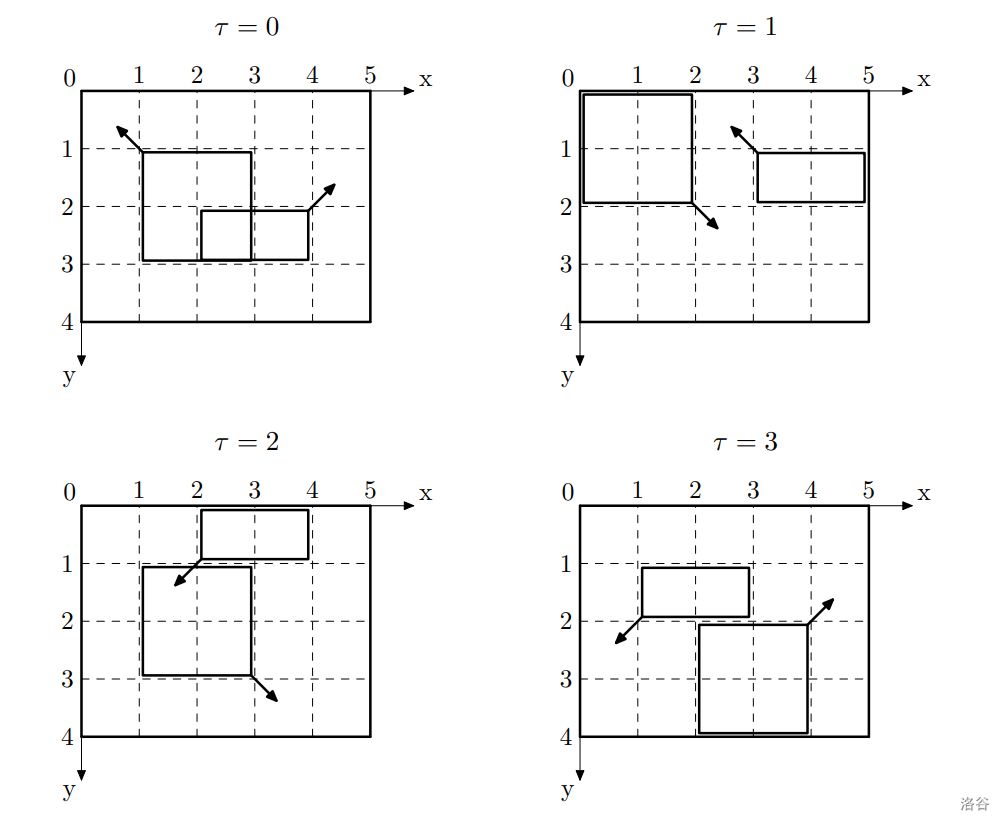
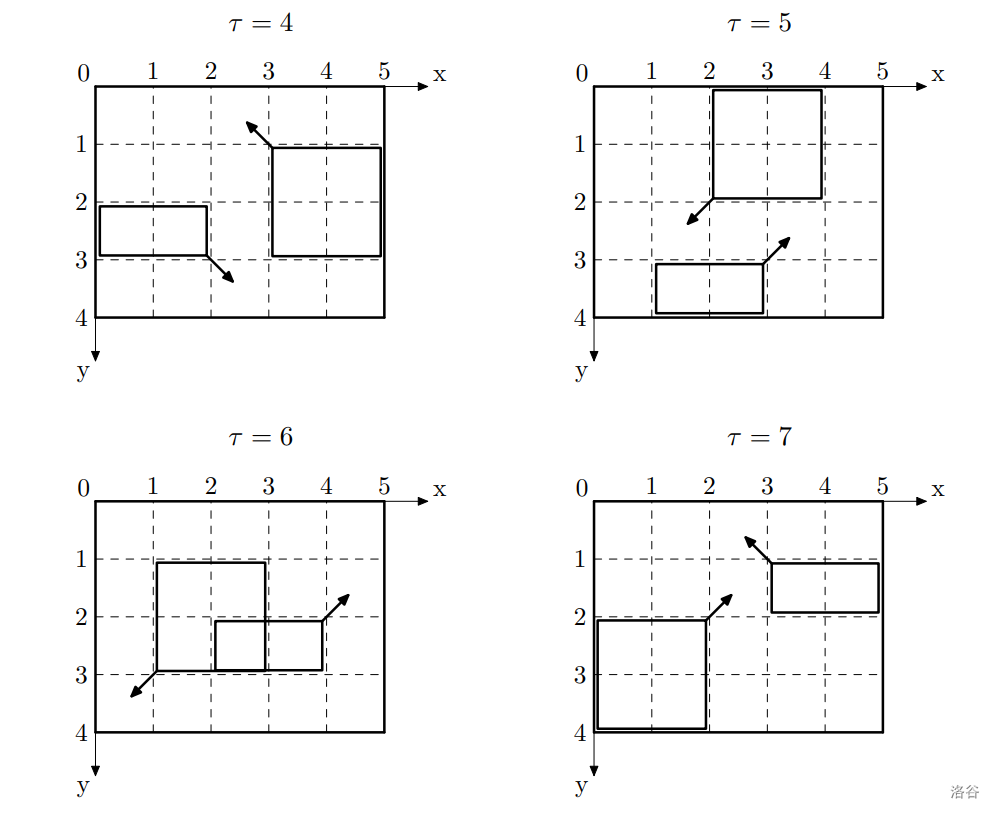
对于第二个测试用例，矩形在最初几秒内的状态如下图所示。矩形在第 $\tau=0$ 秒和第 $\tau=6$ 秒发生重叠。例如，$f(8)=2$。