#P11829. [TOIP2024] 棲息地分配
[TOIP2024] 棲息地分配
Description
有 只猫活动于某个地区,每只猫各有其栖息地,编号为 到 。栖息地之间有 条道路连接,道路总数不超过 。第 条道路连接第 个栖息地和第 个栖息地,猫可以沿着这些道路在栖息地之间双向移动,且不会有两条不同的道路连接着同一对栖息地。有 个动物保护团体要接管此地区,请你协助将这 个栖息地分配给这 个团体,满足以下要求:
- 每个栖息地仅由 个团体管理,且每个团体需要管理至少 个栖息地。每个团体所属的栖息地之间不一定要连通。
- 为了方便管理,每个团体会移除由该团体负责的栖息地之间的道路。换句话说,若有一条道路连接的两个栖息地被分配到同一个团体,该道路会被移除。
- 这些道路移除后,剩余的道路不可以形成「环」,以免猫可能会绕着环奔跑,让工作人员难以捕捉。也就是说,不可以存在一个两两相异的栖息地序列 ,满足 ,且对于所有 ,栖息地 和栖息地 都有一条未被移除的道路连接、同时 和 也有一条未被移除的道路连接。
举例,有 个栖息地,道路连接如下图所示
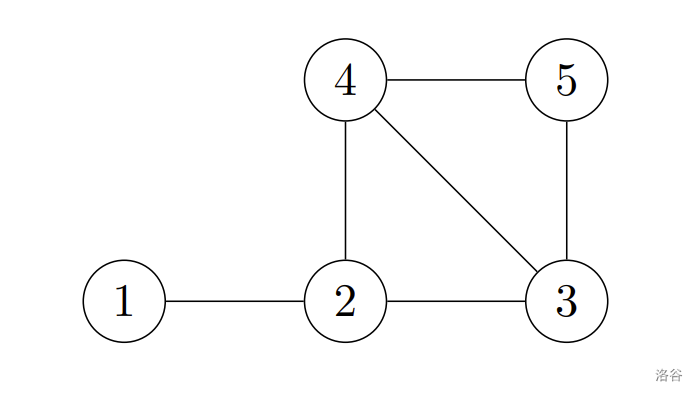
我们可以将第 , , 个栖息地分配给第 个团体,第 个栖息地分配给第 个团体,第 个栖息地分配给第 个团体。 移除掉道路后,如下图所示
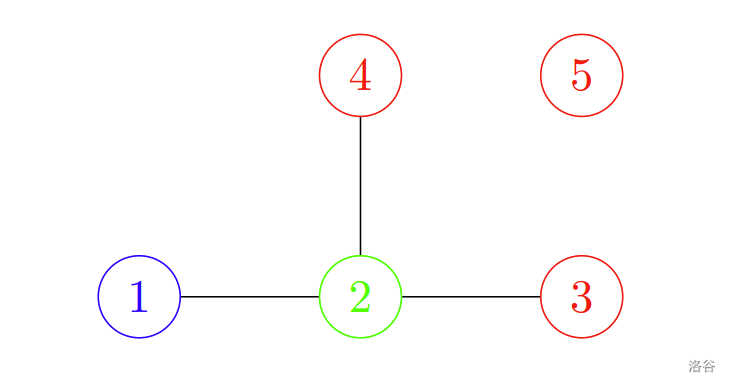
剩余道路不存在环,所以这是一种满足目标的分配方式。
请输出这 个团体应该分别管理哪些栖息地,若有多种分配方式满足条件,输出任意一种。
Input Format
- 表示测试数据个数。
- 为第 组测试数据。
每一组测试数据的输入格式如下:
- 为猫的栖息地数量。
- 为道路数量。
- 为第 条道路连接的栖息地编号。不会有两条不同的道路连接同一对栖息地。
Output Format
输出 组测试数据之答案:
- 为第 组测试数据之答案。
每一组测试数据答案的输出格式如下:
- 为第 个团体分配到的栖息地总数。
- 为第 个团体分配到的第 个栖息地。
若该组测试数据不存在所求的分法,请输出 -1。
1
5 6
1 2
2 3
3 4
4 5
5 3
4 2
3 3 4 5
1 1
1 2
2
5 4
1 2
1 3
3 4
3 5
5 4
1 2
2 3
1 3
4 5
2 1 2
1 3
2 4 5
3 1 2 3
1 4
1 5
Hint
测试数据限制
- 。
- 。
- 。
- ,。
- 所有测试数据中, 的总和不超过 。
评分说明
本题共有四组子任务,条件限制如下所示。 每一组可有一或多组测试数据,该组所有测试数据皆需答对才会获得该组分数。
| 子任务 | 分数 | 额外输入限制 |
|---|---|---|
| 1 | 输入满足 ,且所有的栖息地连通。 | |
| 2 | 输入保证存在两个以上的栖息地互相无法抵达。 | |
| 3 | 输入满足所有测试数据中, 的总和不超过 。 | |
| 4 | 无额外限制。 |

 京公网安备 11011102002149号
京公网安备 11011102002149号