Description
有一个 m 列 n 行 的 01-矩阵恰有 t 个 1,且所有的 1 皆位于同一列。1 所在的列编号为 r,行编号为 c1,c2,…,ct。请计算共有几个 k×k 的子矩阵包含奇数个 0。
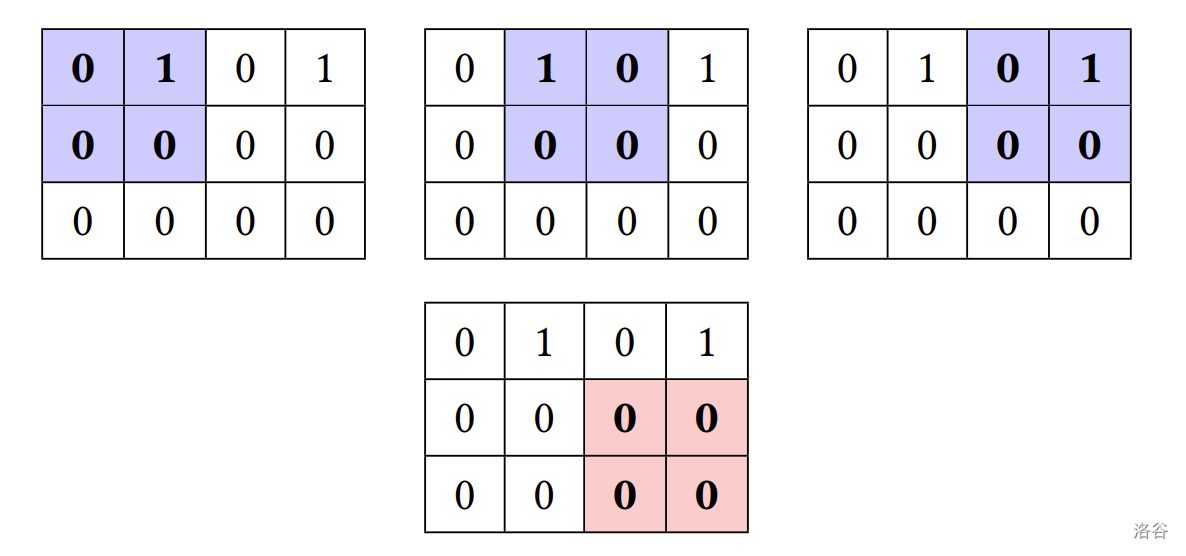
以下图中 3×4 的 01-矩阵为例,共有 3 个 2×2 的子矩阵包含奇数个 0,如蓝色的子矩阵所标示。红色的 2×2 的子矩阵包含 4 个 0,故不列入计算。
m n
t k r
c1 c2 ⋯ ct
- m,n 分别为矩阵之列数与行数。
- t 为 1 的个数。
- k 为子矩阵的大小。
- r 为 t 个 1 所在之列的编号。
- c1,c2,…,ct 为 1 的行的编号,且保证 ci<ci+1。
x
一个整数 x,为含奇数个 0 的 k×k 子矩阵个数。
3 4
2 2 1
2 4
3
4 5
3 3 3
1 3 4
6
Hint
测试数据限制
- 1≤m,n≤109。
- 0≤t≤min(n,105)。
- 1≤k≤min(m,n)。
- 1≤r≤m。
- 1≤ci≤n。
- 输入的数均为整数。
评分说明
本题共有三组子任务,条件限制如下所示。
每一组可有一或多个测试数据,该组所有测试数据皆需答对才会获得该组分数。
| 子任务 |
分数 |
额外输入限制 |
| 1 |
11 |
输入满足 m,n≤1000。 |
| 2 |
41 |
输入满足 m,n≤105。 |
| 3 |
48 |
无额外限制。 |


 京公网安备 11011102002149号
京公网安备 11011102002149号