Description

庞教授正在玩「Tube Master」。

游戏场地被 $(n + 1) \times m$ 条水平管道和 $n \times (m + 1)$ 条垂直管道划分为 $n \times m$ 个单元格。乘积 $nm$ 是一个\textbf{偶数}。管道的交叉点共有 $(n + 1) (m + 1)$ 个。交叉点的二维坐标为 $(i, j)$，其中 $1\le i\le n+1$，$1\le j\le m+1$。我们将坐标为 $(i, j)$ 的交叉点称为交叉点 $(i, j)$。我们将以交叉点 $(i, j), (i+1, j), (i, j+1), (i+1, j+1)$ 为角的单元格称为单元格 $(i, j)$，其中 $1\le i\le n$，$1\le j\le m$。此外，每个单元格 $(i, j)$ 包含一个整数 ${count}_{i, j}$。

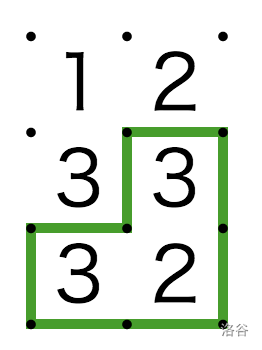
上图展示了一个 $n = 3, m = 2$ 的游戏场地（第三个样例）。

庞教授决定使用一些管道。然而，游戏有几个奇怪的限制条件。

• 每个交叉点要么连接 $0$ 根管道，要么连接 $2$ 根管道。
• 恰好有 ${count}_{i, j}$ 个转折点与单元格 $(i, j)$ 相邻。转折点是指恰好有 $1$ 根水平管道和 $1$ 根垂直管道连接到它的交叉点。转折点 $(x, y)$ 与单元格 $(i, j)$ 相邻是指交叉点 $(x, y)$ 是单元格 $(i, j)$ 的一个角。

使用连接交叉点 $(i, j)$ 和 $(i, j+1)$ 的管道的费用是 $a_{i, j}$。使用连接交叉点 $(i, j)$ 和 $(i+1, j)$ 的管道的费用是 $b_{i, j}$。请帮助庞教授找出他应该使用哪些管道，以便满足限制条件并使总费用最小。

Input Format

第一行包含一个正整数 $T$，表示测试用例的数量。

对于每个测试用例，第一行包含两个整数 $n$ 和 $m$ ($1 \leq n, m \leq 100$)，用一个空格分隔。

接下来的 $n$ 行中，第 $i$ 行包含 $m$ 个整数 ${count}_{i, 1}, {count}_{i, 2}, \dots, {count}_{i, m}$ ($0 \leq {count}_{i, j} \leq 4$)，用空格分隔。

接下来的 $n+1$ 行中，第 $i$ 行包含 $m$ 个整数 ${a}_{i, 1}, {a}_{i, 2}, \dots, {a}_{i, m}$ ($1 \leq {a}_{i, j} \leq 10^9$)，用空格分隔。

接下来的 $n$ 行中，第 $i$ 行包含 $m+1$ 个整数 ${b}_{i, 1}, \mathit{b}_{i, 2}, \dots, {b}_{i, m+1}$ ($1 \leq {b}_{i, j} \leq 10^9$)，用空格分隔。

保证 $nm$ 是一个\textbf{偶数}，且所有测试用例中 $nm$ 的总和不超过 $10^4$。

Output Format

对于每个测试用例，输出一个整数，表示最小费用。

如果没有有效的配置，输出 -1。

4
2 3
4 3 2
2 3 4
2 1 1
2 1 2
1 2 1
1 2 1 2
1 1 1 2
2 2
2 1
2 1
1 2
2 2
1 2
1 2 1
2 1 1
3 2
1 2
3 3
3 2
1 1
1 1
2 2
1 1
1 1 1
1 1 1
2 2 2
2 2
1 2
3 4
5 6
7 8
9 10
11 12 13
14 15 16

13
8
11
-1

Hint

（由 ChatGPT 4o 翻译）