#P9896. [ICPC 2018 Qingdao R] Sub-cycle Graph
[ICPC 2018 Qingdao R] Sub-cycle Graph
Description
Given an undirected simple graph with () vertices and edges where the vertices are numbered from 1 to , we call it a sub-cycle graph if it's possible to add a non-negative number of edges to it and turn the graph into exactly one simple cycle of vertices.
Given two integers and , your task is to calculate the number of different sub-cycle graphs with vertices and edges. As the answer may be quite large, please output the answer modulo .
Recall that
- A simple graph is a graph with no self loops or multiple edges;
- A simple cycle of () vertices is a connected undirected simple graph with vertices and edges, where the degree of each vertex equals to 2;
- Two undirected simple graphs with vertices and edges are different, if they have different sets of edges;
- Let , we denote as an undirected edge connecting vertices and . Two undirected edges and are different, if or .
Input Format
There are multiple test cases. The first line of the input contains an integer (about ), indicating the number of test cases. For each test case:
The first and only line contains two integers and (, ), indicating the number of vertices and the number of edges in the graph.
It's guaranteed that the sum of in all test cases will not exceed .
Output Format
For each test case output one line containing one integer, indicating the number of different sub-cycle graphs with vertices and edges modulo .
3
4 2
4 3
5 3
15
12
90
Hint
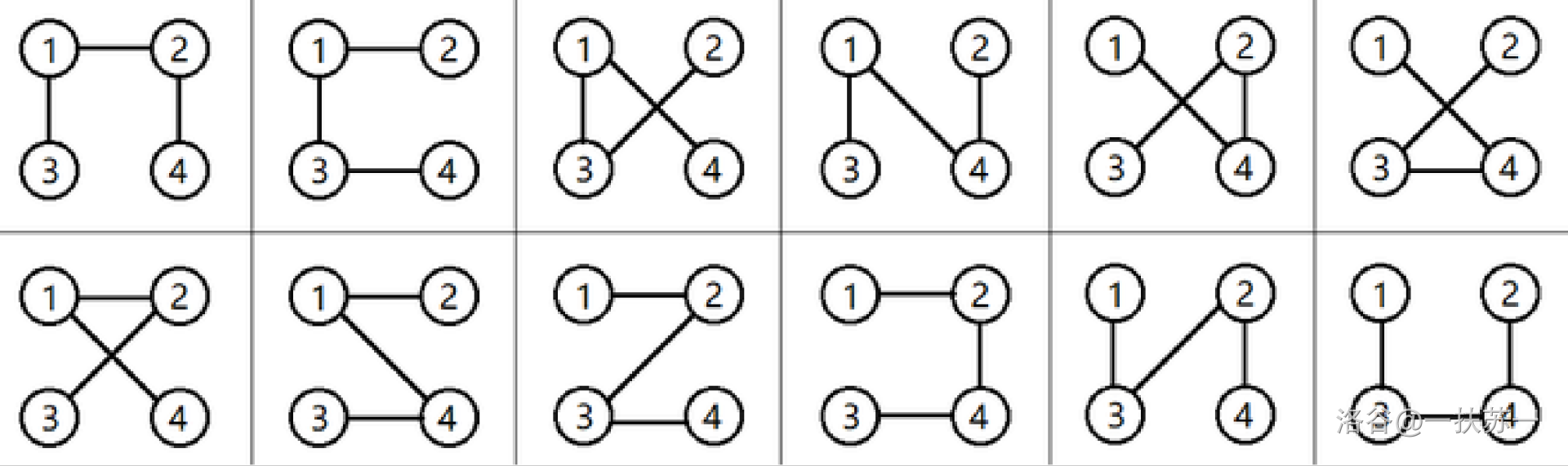
The 12 sub-cycle graphs of the second sample test case are illustrated below.

 京公网安备 11011102002149号
京公网安备 11011102002149号