#P9829. [ICPC 2020 Shanghai R] Traveling Merchant
[ICPC 2020 Shanghai R] Traveling Merchant
Description
Mr. Lawrence is a traveling merchant who travels between cities and resells products. Basically, to earn from it, he needs to buy products at a very low price and sell them at a higher price. Your task is to tell him whether there exists an endless traveling path that can earn money all the time.
To make things simple, suppose there are cities named from to and undirected roads each of which connecting two cities. Mr. Lawrence can travel between cities along the roads. Initially he is located at city and each of the city has a starting price , either or . Due to the law of markets, the price status at city will change (i.e. price will become price, or vice versa) after he departs for a neighboring city from . (City is a neighboring city of city when one of the roads connects city and city .) For some reasons (e.g. product freshness, traveling fee, tax), he :
- Start at city and buy products at city . It is guaranteed that is .
- When he arrives some city, he either sells products or buys products. It is not allowed for him to do nothing before he leaves the city.
- After buying products at some city , he must travel to some neighboring city whose price is and sell the products at city .
- After selling products at some city , he must travel to some neighboring city whose price is and buy the products at city .
As a result, the path will look like an alternation between buy at low price and sell at high price.
An endless earning path is defined as a path consisting of an endless sequence of cities where city and city has a road, , and the price alternates, in other words (indicates a buy-in) and (indicates a sell-out) for . Please note here is the price when city and this value may be different when he arrives the second time.
Your task is to determine whether there exists any such path.
Input Format
There are several test cases. The first line contains a positive integer indicating the number of test cases. Each test case begins with two positive integers and indicating the number of cities and the number of roads.
The next line is a string of length containing H or L. The -th () charactor of is if the starting price at city is . The -th () charactor of is if the starting price at city is .
The -th line () of the following lines contains two different cities and , indicating a road between and .
The sum of the values of over all test cases is no more than . The sum of the values of over all test cases is no more than . For each test case, holds for each . is always . and hold for each . No two roads connect the same pair of cities.
Output Format
For each test case, output a line of yes or no, indicating whether there exists an endless earning path.
2
4 4
LHLH
0 1
1 2
1 3
2 3
3 3
LHH
0 1
0 2
1 2
yes
no
Hint
In the first sample test case, the endless earning path is $0\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow \dots$. In the illustration, cities with price are filled with stripe.

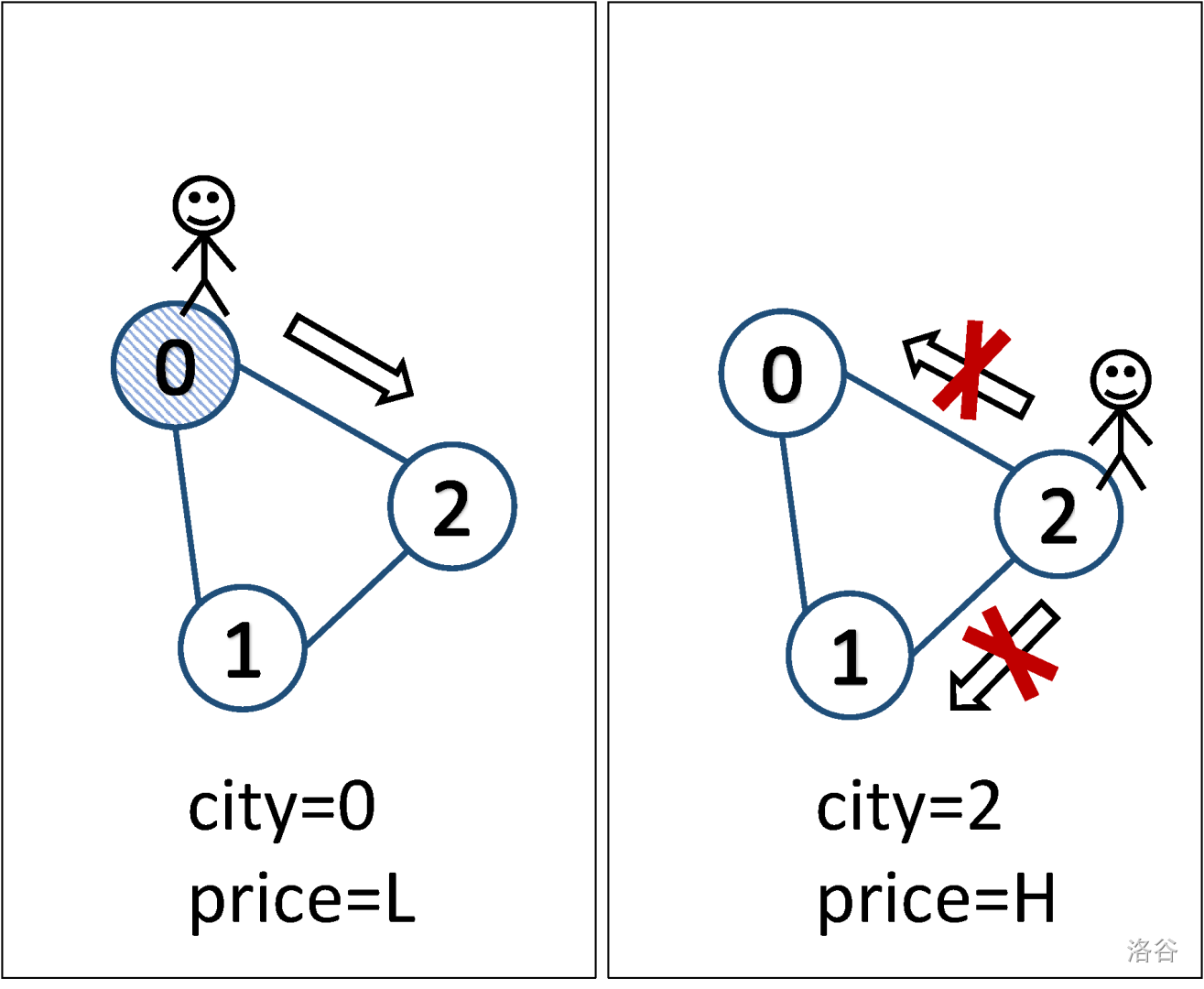
In the second sample test case, Mr. Lawrence can only make one move from city and after that all cities will have price. Thus, no further moves can be made.

 京公网安备 11011102002149号
京公网安备 11011102002149号