题目描述

对于任意长度为 $n$ 的序列 $a$，可以基于 $a$ 建立一个广义线段树。广义线段树是一个有 $(2n-1)$ 个节点的带权二叉树，对于每个编号为 $p$ 的节点，都有两个属性 $L_p$ 和 $R_p$，表示其维护的区间为 $[L_p,R_p]$，同时其权值 $M_p =\prod_{i=L_p}^{R_p}a_i$ 。另外，广义线段树还满足如下性质：

• 所有编号为 $p\in [n,2n-1]$ 的节点是叶节点，同时 $L_p = R_p = p + 1 - n$。
• 所有编号为 $p\in [1,n-1]$ 的节点是非叶节点，其必定有左儿子 $X_p$ 和右儿子 $Y_p$，且 $p < X_p < Y_p$。节点 $p$ 维护的区间为左右儿子维护区间之并，且保证维护区间连续。形式化地，有 $R_{X_p}=L_{Y_p}-1$，且 $L_p=L_{X_p}$，$R_p=R_{Y_p}$。

例如，下面是一个基于 $n=4$ 的序列 $a=\{1, 2, 3, 4\}$ 建立的广义线段树（节点内整数对 $(p,M_p)$ 分别表示编号和权值）。可以发现，广义线段树的形态并不唯一。

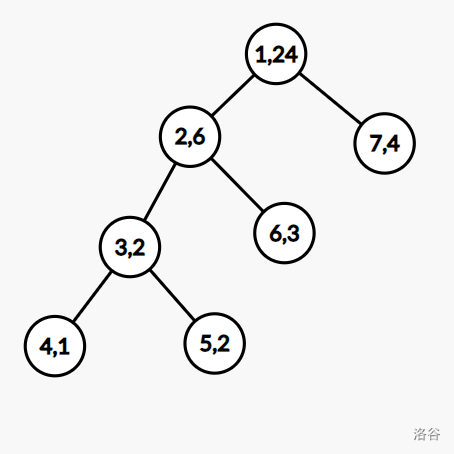
对这个广义线段树而言：

• $[L_7, R_7] = [4, 4]$，故 $M_7 = a_4$
• $[L_6, R_6] = [3, 3]$，故 $M_6 = a_3$
• $[L_5, R_5] = [2, 2]$，故 $M_5 = a_2$
• $[L_4, R_4] = [1, 1]$，故 $M_4 = a_1$
• $[L_3, R_3] = [L_4, R_5] = [1, 2]$，故 $M_3 = a_1 \times a_2$
• $[L_2, R_2] = [L_3, R_6] = [1, 3]$，故 $M_2 = a_1 \times a_2 \times a_3$
• $[L_1, R_1] = [L_2, R_7] = [1, 4]$，故 $M_1 = a_1 \times a_2 \times a_3 \times a_4$

分别给定长度为 $n$ 的序列 $a$，$b$ 以及节点数为 $(2n-1)$ 的广义线段树 $T$ 的形态（即每个节点的左右儿子编号），然后你需要执行 $n$ 次操作，第 $i$ 次操作为将 $a_i$ 变成 $a_i\times b_i$。

每次操作结束后，你需要基于修改后的序列 $a$ 建立与 $T$ 形态相同的广义线段树，并求出所有节点的权值和，即 $\sum_{i=1}^{2n-1}M_i$。由于结果可能会非常大，你只需要求出其对 $998\,244\,353$ 取模后的值。

输入格式

第一行包含一个整数 $n\ (1\le n\le 5\cdot 10^5)$，表示序列 $a$ 和 $b$ 的长度。

第二行包含 $n$ 个整数，其中第 $i$ 个整数定义为 $a_i\ (1 \le a_i < 998\,244\,353)$。

第三行包含 $n$ 个整数，其中第 $i$ 个整数定义为 $b_i\ (1 \le b_i < 998\,244\,353)$。

接下来 $n-1$ 行，其中第 $i$ 行包含两个整数 $X_i,Y_i\ (i<X_i<Y_i\le 2n-1)$，分别表示节点 $i$ 的左右儿子编号。保证输入的广义线段树形态符合题目要求。

输出格式

输出一行用空格间隔的 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 次修改后的答案对 $998\,244\,353$ 取模后的值。

4
1 2 3 4
2 3 2 3
2 7
3 6
4 5

75 207 390 974 

提示

样例中广义线段树的形态和题面中的例子相同。

第一次修改后，$a_1$ 变为 $a_1 \times b_1 = 1 \times 2 = 2$，因而新的 $a = \{2, 2, 3, 4\}$。可以计算出：

• $M_7 = a_4 = 4$
• $M_6 = a_3 = 3$
• $M_5 = a_2 = 2$
• $M_4 = a_1 = 2$
• $M_3 = a_1 \times a_2 = 2 \times 2 = 4$
• $M_2 = a_1 \times a_2 \times a_3 = 2 \times 2 \times 3 = 12$
• $M_1 = a_1 \times a_2 \times a_3 \times a_4 = 2 \times 2 \times 3 \times 4 = 48$

故权值之和为 $M_1 + M_2 + \ldots + M_7 = 75$。

第二次修改后，$a_2$ 变为 $a_2 \times b_2 = 2 \times 3 = 6$。后续的操作与第一次操作类似，此处不再赘述。