题目背景

Z 教授是 C 班的老师。

Z 教授最近发现一个神奇的现象，他的学生竟然都有自己暗恋的对象，但是没有一个人勇于表白。

Z 教授作为过来人，当然懂得每一个学生心里最真实纯真的想法，以及自认为的爱意情愫。Z 教授想起了初恋蕉太狼，他不想让自己的学生在青春年华失去色彩，于是 Z 教授冒着被开除的风险，主动帮助学生表达心意。

然后 Z 教授被开除了。

题目描述

有一棵 $n$ 个节点的内向基环树（保证弱连通），树上每条边都有一个权值。现有一个特定参数 $k$。

由于基环树是内向的，所以一个点 $x$ 可能会有无法直接到达的节点。但是我们可以翻转树上的一些有向边，这样 $x$ 就可以到达树上每一个节点。如果一个节点 $x$ 需要至少翻转 $k$ 条边才能到达 $y$，则称 $y$ 是 $x$ 的乘风破浪点。在翻转了最少的边使得 $x$ 可以到达 $y$ 之后，在 $x$ 到 $y$ 的最短路径上，定义 $F(x, y)$ 为未翻转的边的权值之和，$R(x, y)$ 为已翻转的边的权值之和。

如果 $y$ 是 $x$ 的乘风破浪点，那么有一个值 $G(x, y)$ 表示 $x$ 到 $y$ 的浪涛值，定义 $G(x, y) = F(x, y) \times R(x,y)$。

请你对于每一个节点 $i$，输出 $\sum G(i, y)$ 的值，其中 $y$ 是 $i$ 的乘风破浪点。

输入格式

第一行输入两个正整数 $n, k$，表示基环树大小和一个比较的参数。

接下来 $n$ 行，每行输入 $u, v, w$ 三个正整数，表示树上存在一条边 $(u, v, w)$，表示其起点为 $u$，终点为 $v$，权值为 $w$。

输出格式

输出 $n$ 行，每行一个正整数，表示每个节点到它的所有乘风破浪点的浪涛值之和。

7 1
1 4 3
2 1 2
3 1 6
4 3 4
5 2 4
6 4 1
7 5 2

3
5
105
160
9
176
11

7 1
1 2 3
2 3 2
3 1 2
4 1 3
5 4 2
6 2 1
7 6 4

18
32
46
36
48
40
72

提示

样例解释 #1

拿 $3$ 节点的答案为例子，基环树的形状如图：

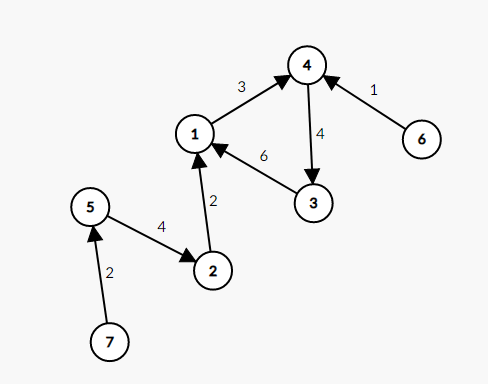
可知 $2,5,6,7$ 为 $3$ 的乘风破浪点，统计答案：

• $G(3, 2) = 6 \times 2 = 12$。

• $G(3, 5) = 6 \times 6 = 36$。

• $G(3, 6) = 9 \times 1 = 9$。

• $G(3, 7) = 6 \times 8 = 48$。

所以 $\sum G(3, j) = 12 + 36 + 9 + 48$，答案为 $105$。

数据范围

本题采用捆绑测试。

• Subtask 1（5 points）：$1 \leqslant n \leqslant 10$，包含特殊性质。
• Subtask 2（10 points）：$1 \leqslant n \leqslant 5000$，包含特殊性质。
• Subtask 3（25 points）：$1 \leqslant n \leqslant 10^5$，包含特殊性质。
• Subtask 4（60 points）：$1 \leqslant n \leqslant 10^6$，无特殊限制。

特殊性质：保证环上节点的个数在 $10^3$ 以内。

对于所有数据，$1 \leqslant n \leqslant 10^6$，$1 \leqslant k \leqslant 10$，保证答案不会超过 $10^{18}$。