题目描述

Given a convex polygon $P$ with $n$ vertices, you need to choose two vertices of $P$, so that the line connecting the two vertices will split $P$ into two smaller polygons $Q$ and $R$, both with positive area.

Let $d(Q)$ be the diameter of polygon $Q$ and $d(R)$ be the diameter of polygon $R$, calculate the minimum value of $(d(Q))^2 + (d(R))^2$.

Recall that the diameter of a polygon is the maximum distance between two points inside or on the border of the polygon.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$ indicating the number of test cases. For each test case:

The first line contains an integer $n$ ($4 \le n \le 5 \times 10^3$) indicating the number of vertices of the convex polygon $P$.

For the following $n$ lines, the $i$-th line contains two integers $x_i$ and $y_i$ ($0 \le x_i, y_i \le 10^9$) indicating the $i$-th vertex of the convex polygon $P$. Vertices are given in counter-clockwise order. It's guaranteed that the area of the convex polygon is positive, and there are no two vertices with the same coordinate. It's possible that three vertices lie on the same line.

It's guaranteed that the sum of $n$ of all test cases will not exceed $5 \times 10^3$.

输出格式

For each test case output one line containing one integer indicating the answer.

题目大意

【题目描述】

给定一个有 $n$ 个顶点的凸多边形 $P$，您需要选择 $P$ 的两个顶点，并用一条同时穿过这两个顶点的直线，将 $P$ 分成两个面积均为正数的小多边形 $Q$ 和 $R$。

记 $d(Q)$ 表示多边形 $Q$ 的直径，$d(R)$ 表示多边形 $R$ 的直径，求 $(d(Q))^2 + (d(R))^2$ 的最小值。

请回忆：一个多边形的直径，指的是该多边形内部或边界上任意两点之间的距离的最大值。

【输入格式】

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数。对于每组测试数据：

第一行输入一个整数 $n$（$4 \le n \le 5 \times 10^3$）表示凸多边形 $P$ 的顶点数量。

对于接下来 $n$ 行，第 $i$ 行输入两个整数 $x_i$ 和 $y_i$（$0 \le x_i, y_i \le 10^9$），表示凸多边形 $P$ 的第 $i$ 个顶点。顶点按逆时针顺序给出。保证该凸多边形面积为正，且没有顶点会重合。可能存在三个顶点位于同一条直线上的情况。

保证所有数据 $n$ 之和不超过 $5 \times 10^3$。

【输出格式】

每组数据输出一行一个整数表示答案。

【样例解释】

第一组样例数据如下图所示。小多边形的直径用红色虚线标出。事实上，顶点 $(1, 0)$ 和 $(1, 1)$ 是这一组数据中唯一能选择的一对顶点。您不能选择顶点 $(0, 0)$ 和 $(2, 0)$，或顶点 $(0, 0)$ 和 $(1, 1)$，因为它们无法将 $P$ 分成两个面积均为正数的小多边形。

第二组样例数据如下图所示。小多边形的直径用红色虚线标出。

2
4
1 0
2 0
1 1
0 0
6
10 4
9 7
5 7
4 5
6 4
9 3

4
44

提示

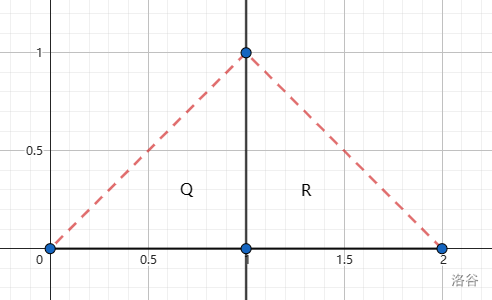
The first sample test case is shown as follows. The diameter of smaller polygons are marked by red dashed segments. In fact, $(1, 0)$ and $(1, 1)$ are the only pair of vertices we can choose in this test case. You can't choose $(0, 0)$ and $(2, 0)$, or $(0, 0)$ and $(1, 1)$, because they can't split $P$ into two smaller polygons both with positive area.

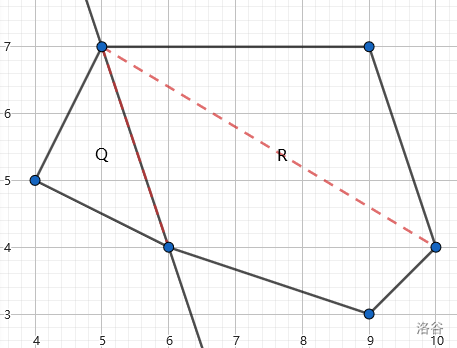
The second sample test case is shown as follows. The diameter of smaller polygons are marked by red dashed segments.