#P9701. [GDCPC 2023] Classic Problem
[GDCPC 2023] Classic Problem
Description
Given an undirected complete graph with vertices and triples where , it's guaranteed that , and for any two triples and with different indices we have .
For any two vertices and in the graph (), define the weight of the edge connecting them as follows:
- If there exists a triple satisfying and , the weight of edge will be .
- Otherwise, the weight of edge will be .
Calculate the total weight of edges in the minimum spanning tree of the graph.
Input Format
There are multiple test cases. The first line of the input contains an integer () indicating the number of test cases. For each test case:
The first line contains two integers and (, ) indicating the number of vertices in the graph and the number of triples.
For the following lines, the -th line contains three integers , and (, ) indicating the -th triple. It's guaranteed that for all we have .
It's guaranteed that the sum of of all test cases will not exceed .
Output Format
For each test case output one line containing one integer indicating the total weight of edges in the minimum spanning tree of the graph.
3
5 3
1 2 5
2 3 4
1 5 0
5 0
5 4
1 2 1000000000
1 3 1000000000
1 4 1000000000
1 5 1000000000
4
4
1000000003
Hint
The first sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.
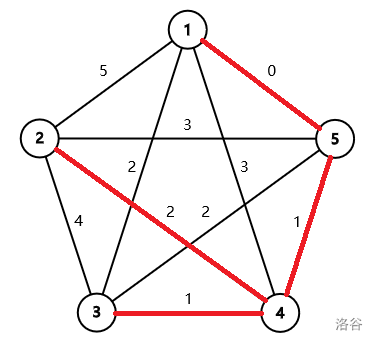
The second sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.
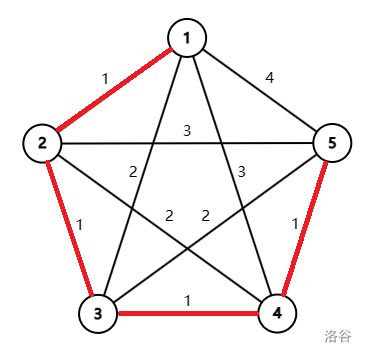
The third sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.
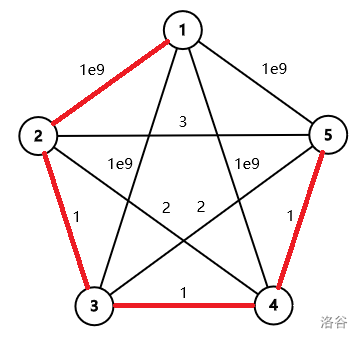

 京公网安备 11011102002149号
京公网安备 11011102002149号