题目描述

Given a grid with $n$ rows and $n$ columns, there is exactly one black cell in the grid and all other cells are white. Let $(i, j)$ be the cell on the $i$-th row and the $j$-th column, this black cell is located at $(b_i, b_j)$.

You need to cover all white cells with some L-shapes, so that each white cell is covered by exactly one L-shape and the only black cell is not covered by any L-shape. L-shapes must not exceed the boundary of the grid.

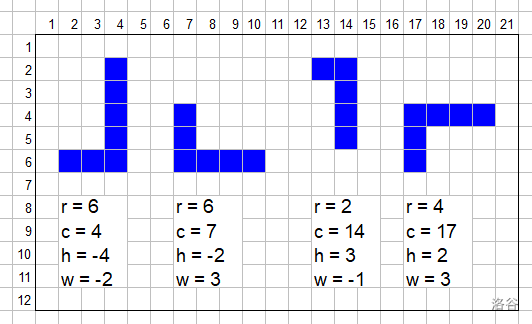
More formally, an L-shape in the grid is uniquely determined by four integers $(r, c, h, w)$, where $(r, c)$ determines the turning point of the L-shape, and $h$ and $w$ determine the direction and lengths of the two arms of the L-shape. The four integers must satisfy $1 \le r, c \le n$, $1 \le r + h \le n$, $1 \le c + w \le n$, $h \ne 0$, $w \ne 0$.

• If $h < 0$, then all cells $(i, c)$ satisfying $r + h \le i \le r$ belong to this L-shape; Otherwise if $h > 0$, all cells $(i, c)$ satisfying $r \le i \le r + h$ belong to this L-shape.
• If $w < 0$, then all cells $(r, j)$ satisfying $c + w \le j \le c$ belong to this L-shape; Otherwise if $w > 0$, all cells $(r, j)$ satisfying $c \le j \le c + w$ belong to this L-shape.

The following image illustrates some L-shapes.

输入格式

There is only one test case in each test file.

The first line contains three integers $n$, $b_i$ and $b_j$ ($1 \le n \le 10^3$, $1 \le b_i, b_j \le n$) indicating the size of the grid and the position of the black cell.

输出格式

If a valid answer exists first output Yes in the first line, then in the second line output an integer $k$ ($0 \leq k \leq \frac{n^2-1}{3}$) indicating the number of L-shapes to cover white cells. Then output $k$ lines where the $i$-th line contains four integers $r_i$, $c_i$, $h_i$, $w_i$ separated by a space indicating that the $i$-th L-shape is uniquely determined by $(r_i, c_i, h_i, w_i)$. If there are multiple valid answers you can print any of them.

If there is no valid answer, just output No in one line.

题目大意

【题目描述】

给定一个 $n$ 行 $n$ 列的网格，网格中包含恰好一个黑色方格，其余方格均为白色。令 $(i, j)$ 表示位于第 $i$ 行第 $j$ 列的格子，这个黑色方格位于 $(b_i, b_j)$。

您需要用若干 L 形覆盖所有白色格子，使得每个白色格子都恰好被一个 L 形所覆盖，同时唯一的黑色方格不能被任何 L 形覆盖。L 形不能超过网格的边界。

更正式地，网格中的一个 L 形由四个整数 $(r, c, h, w)$ 唯一确定，其中 $(r, c)$ 确定了 L 形的转折点，$h$ 和 $w$ 确定了 L 形两臂的方向和长度。四个整数满足 $1 \le r, c \le n$，$1 \le r + h \le n$，$1 \le c + w \le n$，$h \ne 0$，$w \ne 0$。

• 若 $h < 0$，则所有满足 $r + h \le i \le r$ 的格子 $(i, c)$ 均属于该 L 形；否则若 $h > 0$，则所有满足 $r \le i \le r + h$ 的格子 $(i, c)$ 均属于该 L 形。
• 若 $w < 0$，则所有满足 $c + w \le j \le c$ 的格子 $(r, j)$ 均属于该 L 形；否则若 $w > 0$，则所有满足 $c \le j \le c + w$ 的格子 $(r, j)$ 均属于该 L 形。

下图展示了几种 L 形。

【输入格式】

每个测试文件仅有一组测试数据。

第一行输入三个整数 $n$，$b_i$，$b_j$（$1 \le n \le 10^3$，$1 \le b_i, b_j \le n$）表示网格的大小以及黑色格子的位置。

【输出格式】

如果存在符合要求的覆盖方案，首先输出一行 Yes，接下来在第二行输出一个整数 $k$（$0 \leq k \leq \frac{n^2-1}{3}$）表示覆盖白色格子的 L 形数量。接下来输出 $k$ 行，第 $i$ 行输出四个由单个空格分隔的整数 $r_i$，$c_i$，$h_i$ 和 $w_i$，表示第 $i$ 个 L 形由 $(r_i, c_i, h_i, w_i)$ 唯一确定。如果有多种合法答案，您可以输出任意一种。

如果不存在符合要求的覆盖方案，仅需要输出一行 No。

【样例解释】

第一组样例数据展示如下。

5 3 4

Yes
6
5 1 -1 3
1 2 1 3
3 1 -2 1
4 3 -1 -1
4 5 1 -1
2 5 1 -2

1 1 1

Yes
0

提示

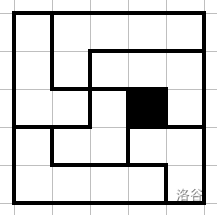
We illustrate the first sample test case as follows.