#P9565. [SDCPC 2023] Not Another Path Query Problem
[SDCPC 2023] Not Another Path Query Problem
Description
After reading the paper Distributed Exact Shortest Paths in Sublinear Time, you have learned how to solve the distributed single-source shortest paths problem in . To give your knowledge good practice, Little Cyan Fish prepared the following practice task for you.
Little Cyan Fish has a graph consisting of vertices and bidirectional edges. The vertices are numbered from to . The -th edge connects vertex to vertex and is assigned a weight .
For any path in the graph between two vertices and , let's define the value of the path as the bitwise AND of the weights of all the edges in the path.
As a fan of high-value paths, Little Cyan Fish has set a constant threshold . Little Cyan Fish loves a path if and only if its value is at least .
Little Cyan Fish will now ask you queries, where the -th query can be represented as a pair of integers . For each query, your task is to determine if there exists a path from vertex to vertex that Little Cyan Fish would love it.
Input Format
There is only one test case in each test file.
The first line contains four integers , , and (, , , ) indicating the number of vertices, the number of edges, the number of queries and the constant threshold.
For the following lines, the -th line contains three integers , and (, , ), indicating a bidirectional edge between vertex and vertex with the weight . There might be multiple edges connecting the same pair of vertices.
For the following lines, the -th line contains two integers and (, ), indicating a query.
Output Format
For each query output one line. If there exists a path whose value is at least between vertex and output Yes, otherwise output No.
9 8 4 5
1 2 8
1 3 7
2 4 1
3 4 14
2 5 9
4 5 7
5 6 6
3 7 15
1 6
2 7
7 6
1 8
Yes
No
Yes
No
3 4 1 4
1 2 3
1 2 5
2 3 2
2 3 6
1 3
Yes
Hint
We now use to represent the bitwise AND operation.
The first sample test case is shown as follows.
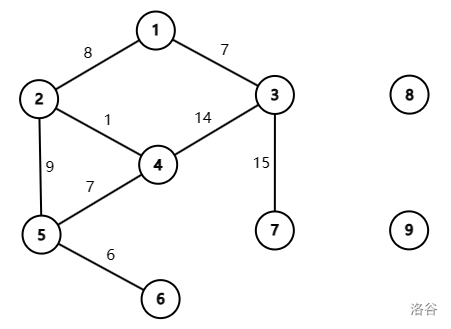
- For the first query, a valid path is , whose value is .
- For the third query, a valid path is , whose value is .
- For the fourth query, as there is no path between vertex and , the answer is
No.
For the only query of the second sample test case, we can consider the path consisting of the -nd and the -th edge. Its value is .

 京公网安备 11011102002149号
京公网安备 11011102002149号