Description

浣熊岭的森林可以看作一张 $n \times m$ 的网格图。工厂排放的废水污染了纵贯森林的梦枫溪（一条直线），导致所经区域对浣熊是有害的。小浣熊 CleverRaccoon 为了研究废水对浣熊的危害，要寻求你的帮助。

设 $f(n,m)$ 表示一条直线最多能穿过 $n\times m$ 的网格图的格子数。

小浣熊有两种问题想要问你：

1. 给定 $n,m$，求 $f(n,m)$；
2. 给定 $n,m,Q$，你需要找到 $n'\ge n,m'\ge m$，满足 $f(n',m')\ge Q$，且 $n'\times m'$ 尽可能小。求 $n'm'-nm$ 的最小值对 $998244353$ 取模的结果。数据保证 $f(n,m)<Q$。

Input Format

本题包含多组测试数据。

第一行，输入一个正整数 $T$，表示有 $T$ 次询问。

对于每次询问：

第一行，输入一个正整数 $op$，表示问题类型。

第二行，若 $op=1$，输入 $2$ 个正整数 $n$ 和 $m$；若 $op=2$，输入 $3$ 个正整数 $n$、$m$ 和 $Q$。

Output Format

共 $T$ 行，对于每次询问：一行输出 $1$ 个正整数，表示对应问题的答案。

2
1
2 3
2
2 3 10

4
12

Hint

样例解释 #1

对于第一次询问：

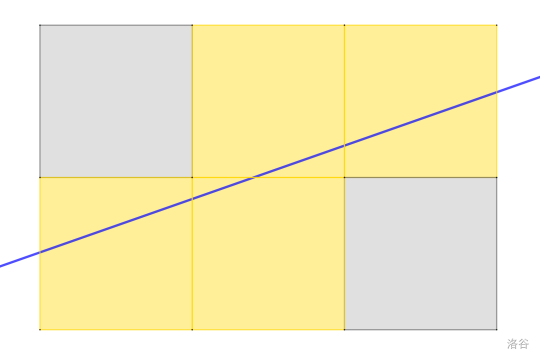
下图所示的情况是一种最佳构造方案，梦枫溪穿过 $2 \times 3$ 的网格森林时，最多穿过 $4$ 个小网格（黄色部分为穿过的网格，灰色部分为未穿过的网格）。

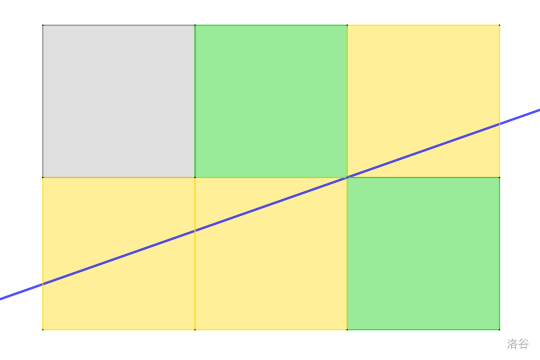
下示方案不是一种最佳方案，梦枫溪是从两个绿色网格中间的一个顶点上穿过的，所以两个绿色区域都没有被穿过。因此梦枫溪只穿过了 $3$ 个小网格。

对于第二次询问：

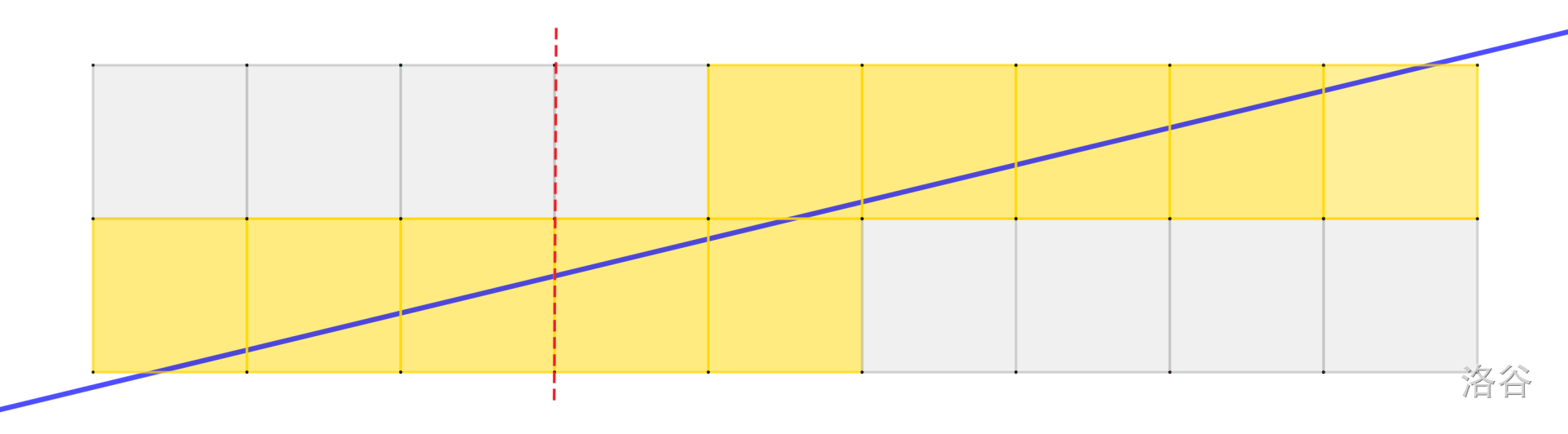
如下图所示，当 $n'=2$, $m'=9$ 时，才能使梦枫溪穿过 $10$ 个网格的情况下，在原基础添加的 $n'm'-nm$ 个网格是最少的（红色虚线左边是原来的森林，右边是添加的部分）。

数据范围

本题采用 Subtask 捆绑测试。

对于 $100\%$ 的数据，保证 $1 \le T \le 10$，$op \in \{1,2\}$，$1 \le n,m \le 10^{18}$，$2 \le n+m \le Q \le 2 \times 10^{18}$。