题目背景

译自 JOI Open 2023 T2 「セルオートマトン / Cell Automaton」

题目描述

我们有一个充分大的二维网格，网格由从上到下和从左到右的正方形单元格密铺而成。

有一个单元格是坐标原点。令 $(x,y)$ 表示表示从原点向右移动 $x$ 个单元格，再向上移动 $y$ 个单元格所到达的单元格。这里，向左移动 $a$ 个单元格意味着向右移动 $-a$ 个单元格。类似地，向下移动 $a$ 个单元格意味着向上移动 $-a$ 个单元格。

在时刻 $0$，单元格 $(X_1,Y_1),(X_2,Y_2),\ldots,(X_N,Y_N)$ 是黑色的，其余单元格是白色的。

对于 $t=0,1,2,\ldots$，根据单元格在 $t$ 时刻的颜色，单元格在 $t+1$ 时刻的颜色按如下方法确定：

• 如果在时刻 $t$ 时单元格是黑色，那么在时刻 $t+1$ 这个单元格变为灰色。
• 如果在时刻 $t$ 时单元格是灰色，那么在时刻 $t+1$ 这个单元格变为白色。
• 如果在时刻 $t$ 时单元格是白色，并且与其相邻的四个单元格（即，与其共边的四个单元格）中至少有一个在时刻 $t$ 是黑色的，那么在时刻 $t+1$ 这个单元格变为黑色。否则，它将在时刻 $t+1$ 保持白色。

你有 $Q$ 次查询。对于第 $j$ 个查询，你应该回答在时刻 $T_j$ 时有多少黑色单元格。

给定在时刻 $0$ 时的单元格颜色信息和查询，写一个程序回答询问。

输入格式

第一行两个整数 $N,Q$。

接下来 $N$ 行，每行两个整数 $X_i,Y_i$。

接下来 $Q$ 行，每行一个整数 $T_j$。

输出格式

输出 $Q$ 行，每行一个整数，表示在时刻 $T_j$ 时有多少黑色单元格。

2 3
0 2
1 0
0
1
2

2
8
12

3 5
0 0
2 2
5 5
0
1
2
3
4

3
12
21
24
26

4 10
-3 -3
3 3
-4 4
4 -4
0
1
2
3
4
5
6
7
8
9

4
16
32
48
56
56
55
56
60
64

提示

【样例解释 #1】

下图展示了在时刻 $0$ 时的单元格情况。因为有 $2$ 个黑色单元格，所以第一个询问的回答是 $2$。

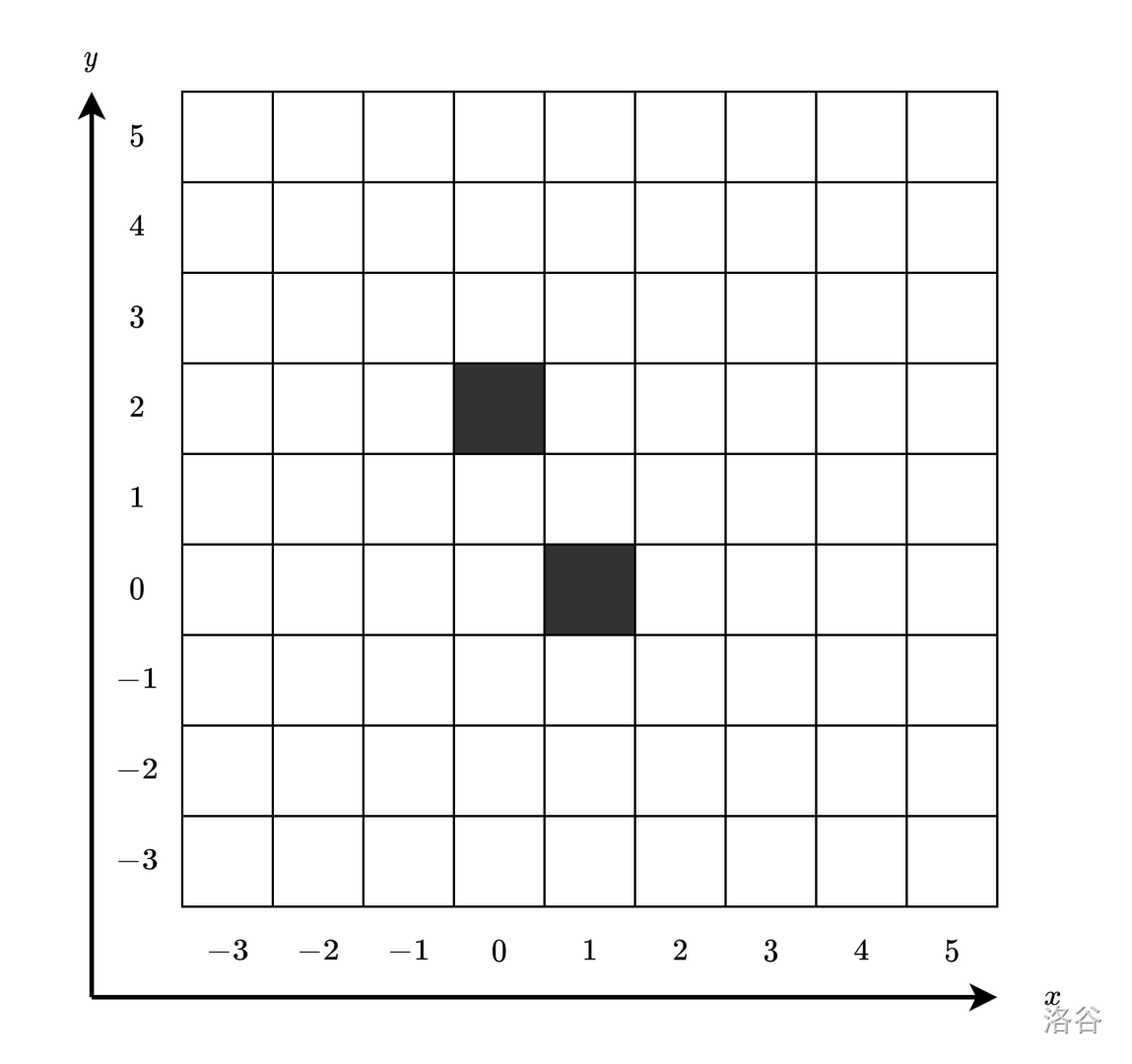
下图展示了在时刻 $1$ 时的单元格情况。因为有 $8$ 个黑色单元格，所以第二个询问的回答是 $8$。

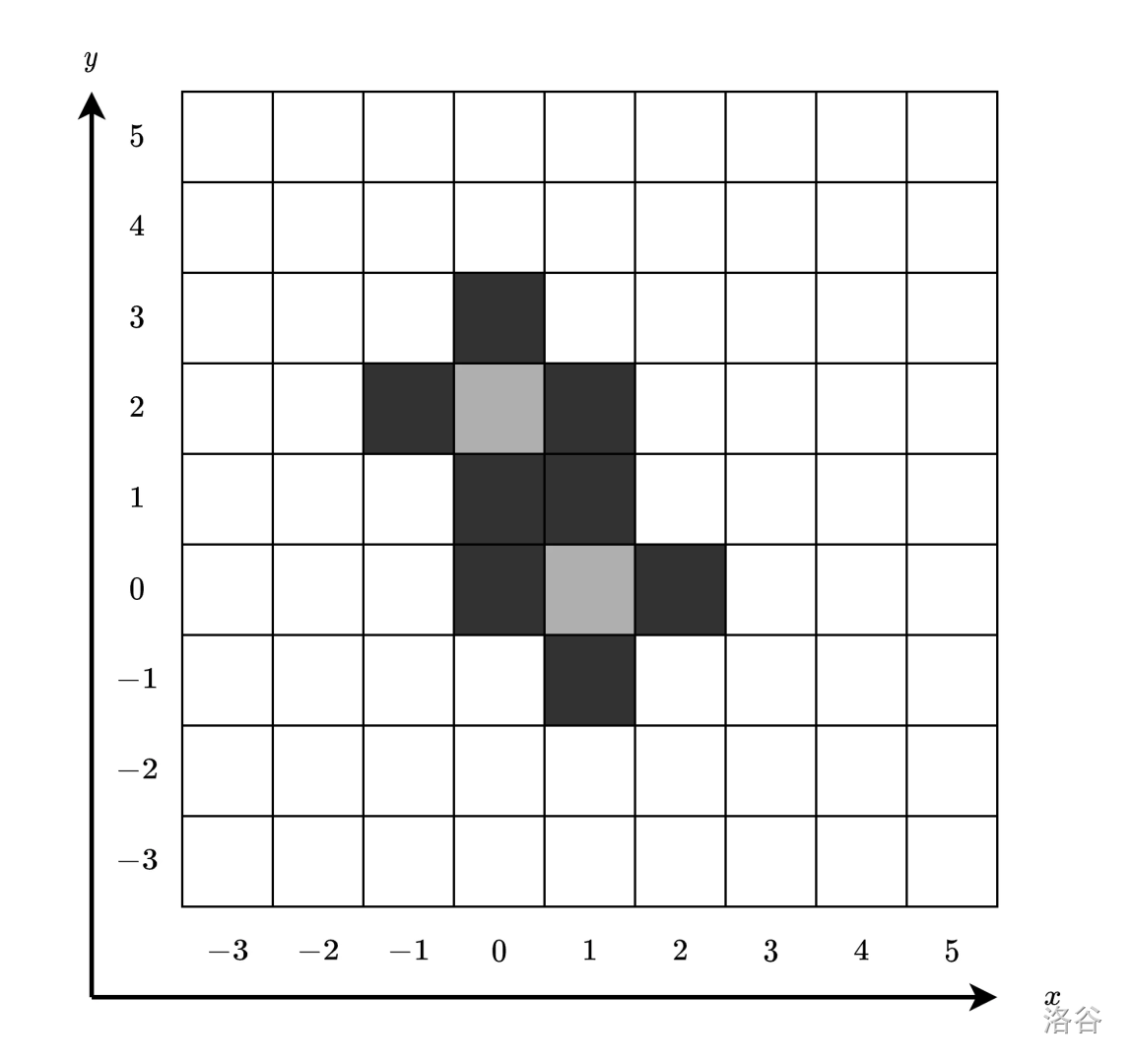
下图展示了在时刻 $2$ 时的单元格情况。因为有 $12$ 个黑色单元格，所以第三个询问的回答是 $12$。

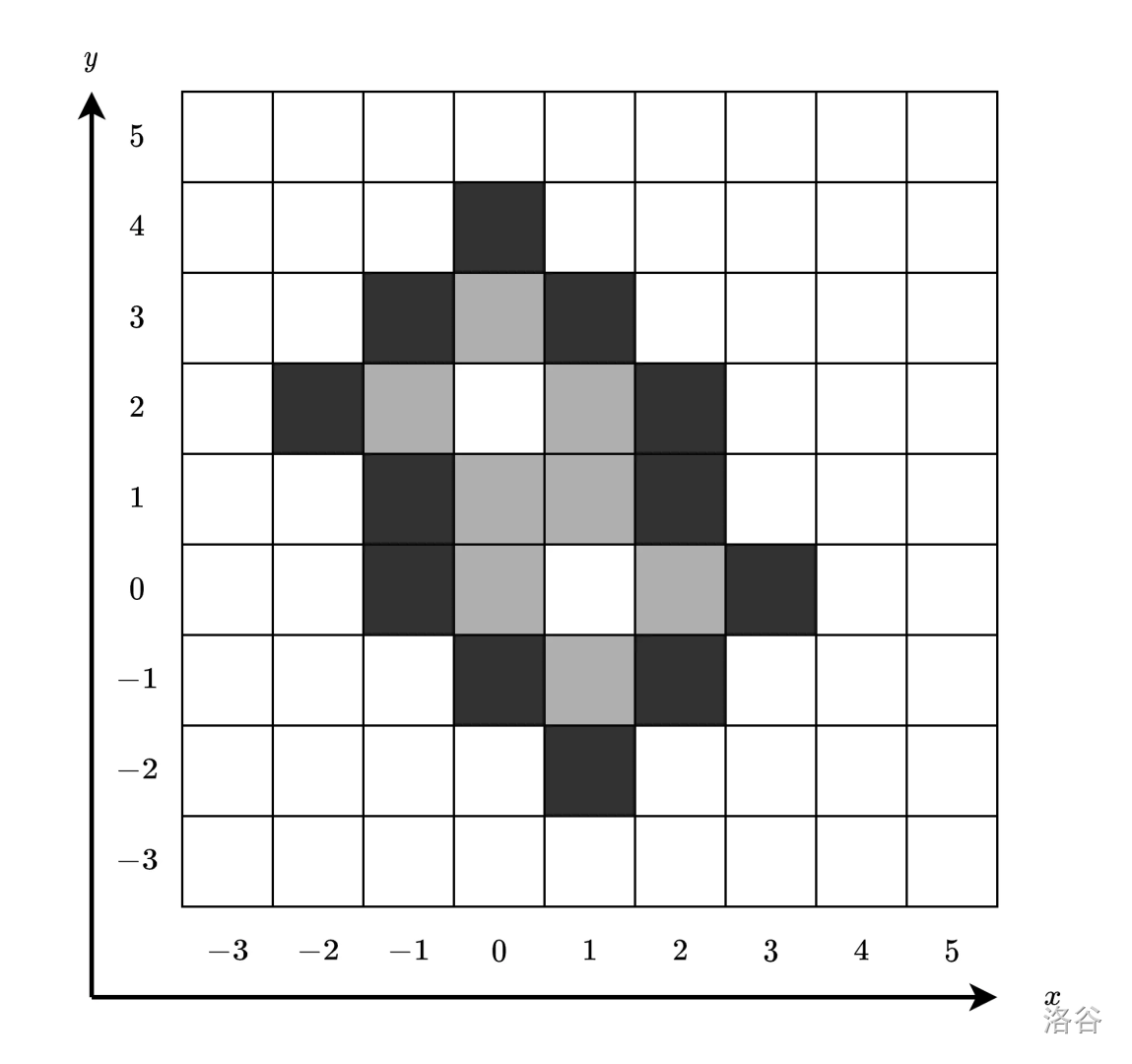
这组样例满足子任务 $1,2,6,7$ 的限制。

【样例解释 #2】

这组样例满足子任务 $1,2,4,6,7$ 的限制。

【样例解释 #3】

这组样例满足子任务 $1,2,6,7$ 的限制。

【数据范围】

对于所有数据，满足：

• $1\le N\le 10^5$
• $1\le Q\le 5\times 10^5$
• $|X_i|,|Y_i|\le 10^9$
• $(X_i,Y_i)\neq (X_j,Y_j)\ (1\le i < j\le N)$
• $0\le T_j\le 10^9$
• $T_j<T_{j+1}$

详细子任务附加限制及分值如下表所示。

子任务	附加限制	分值
$1$	$\lvert X_i\rvert ,\lvert Y_i\rvert \le 50,T_j\le 50$	$4$
$2$	$\lvert X_i\rvert ,\lvert Y_i\rvert \le 1\ 000,T_j\le 1\ 000$	$12$
$3$	$X_i=Y_i,Q=1$	$8$
$4$	$X_i=Y_i$
$5$	$N\le 2\ 000,Q=1$	$17$
$6$	$N\le 2\ 000$	$25$
$7$	无附加限制	$26$