题目背景

— rs8

题目描述

【简要题意】

给定一棵 $n$ 个节点的无根树以及树上的 $k$ 个关键节点，边有边权（即边的长度）。$q$ 次询问，每次给出 $s,t$，问从 $s$ 到 $t$ 且经过至少一次每个关键节点的路径的最短长度。

【原始题意】

在某一面 kid 又遇到了往返跑关卡。Really popular apparently.

关卡给 kid 留下的空间形状是一棵无向带权树，边权即边的长度。这棵树有 $n$ 个节点，其中有 $k$ 个点上各恰有一个发光小球，kid 经过有小球的点（称为关键点）时就可以收集小球。kid 从 $s$ 点出发，当他收集到全部 $k$ 个小球时，传送门就会在 $t$ 点出现。

想速通的 kid 想知道他从 $s$ 点出发收集到全部 $k$ 个小球并进入位于 $t$ 点的传送门所需要走的最小时间（其实也就是路径长度，因为 kid 的速度恒定）。

但是 Geezer 很狡猾，塔内这一面被复制成了 $q$ 层，每层的 $s$ 和 $t$ 还可能有变动。kid 慌了，忙找到你求助。

输入格式

第一行三个正整数 $n, q, k$，表示树的节点个数，询问次数和关键节点个数。

接下来 $n-1$ 行，每行三个正整数 $u, v, w$，表示树中存在边 $(u, v)$，边权为 $w$。保证输入构成一棵树。

接下来一行 $k$ 个两两不同的正整数，表示关键节点的编号。

接下来 $q$ 行，每行两个正整数 $s, t$，表示一次询问。

输出格式

对于每次询问输出一行一个非负整数，表示此次询问的最短合法路径长度。

注意，合法路径可以不经过任何边，此时路径长为 $0$。

7 5 2
1 2 3
1 3 5
3 4 2
3 5 4
2 6 1
1 7 1
2 3
2 3
2 1
7 1
4 5
6 6

8
13
17
22
18

提示

【数据范围】

本题采用捆绑测试。

$$\def\r{\cr\hline} \def\None{\text{None}} \def\arraystretch{1.5} \begin{array}{c|c|c|c} \textbf{Subtask} & \text{测试点编号} & \textbf{Sp. Constraints} & \textbf{Score}\r \textsf1&1\sim14 & n\leqslant15,\mathbf R& 18 \r \textsf2&15\sim20 & q=1 & 18 \r \textsf3&46\sim48 & s=t,k=n & 6 \r \textsf4&21\sim25 & k=n & 18 \r \textsf5&26\sim30 & \mathbf A & 18 \r \textsf6&31\sim45 & - & 22 \r \end{array} $$

友情提醒：$\text{Subtask }\textsf1$ 并没有限制 $q$ 的范围。

• 特殊性质 $\mathbf R$：保证树随机生成（对于 $i\ge2$，在 $[1,i)$ 内随机选择一个点和 $i$ 连边，边权在一固定区间内均匀随机生成）。
• 特殊性质 $\mathbf A$：定义 $f(x)$ 表示存在 $i,j\in[1,n]$（可能 $i=j$） 且 $i,j$ 均为关键点，使得 $x$ 在 $i$ 到 $j$ 的最短路径上；那么对每次询问保证 $f(s)$ 和 $f(t)$ 均成立。

对于 $100\%$ 的数据，$1\leqslant n\leqslant 10^5$，$1\leqslant q\leqslant 10^5$，$1\leqslant k\leqslant n$，$1\leqslant w\leqslant 10^4$，$1\leqslant u,v,s,t\leqslant n$。

【样例解释 #1】

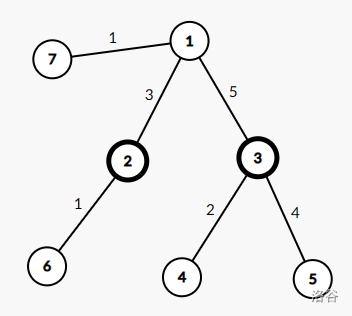
图中加粗节点表示关键点。

对于每组询问，以下为一种最优路径（最优路径可能有多条）：

1. $2\to1\to3$。
2. $2\to1\to3\to1$。
3. $7\to1\to2\to1\to3\to1$。
4. $4\to3\to1\to2\to1\to3\to5$。
5. $6\to2\to1\to3\to1\to2\to6$。