题目背景

题目描述

【简要题意】

给定 $n,m,k,S$，请构造长度为 $n$ 的整数序列 $a$ 使得：

• $0\leqslant a_i\leqslant m,\forall i\in[1,n]$（即序列 $a$ 内的每个元素均不小于 $0$ 且不大于 $m$）。
• $|a_i-a_{i-1}|\leqslant k,\forall i\in(1,n]$（即序列 $a$ 内的每两个相邻元素之差的绝对值均不大于 $k$）。
• $(\sum_{i=1}^n a_i ) = S$（即序列 $a$ 内的所有元素的和为 $S$）。

保证有解。

【原始题意】

前面忘了，但是你随 kid 穿越到了 ic（I wanna be the Creator），来到了一个关卡编辑器面前。该地图宽为 $n$，高为 $(m+1)$，是你不能修改的；里面还有 $S$ 个 $1\times1$ 大小的未摆放的砖。现在你需要帮 kid 摆好这一面，也就是说，将这 $S$ 个砖摆放好，使得他可以通过。有以下要求：

1. 砖是有重力的，所以一块砖只能摆放在下边界上或者另一块砖上。同一横纵坐标不能摆放多块砖。
2. 你至少要给 kid 留一条缝来通过，所以每一列你最高只能放 $m$ 块砖（地图高度为 $m+1$）。但是注意，ic 关卡下边界没有伤害，某一列是可以不放砖块的。
3. kid 的跳跃能力和从高处坠落而不受伤的能力是有限的，这用一个非负整数 $k$ 来描述：相邻两列摆放的砖的数量之差的绝对值不能超过 $k$，否则该关卡对 kid 来说就是无解的。（但是注意：该条对第一列高度没有要求，kid 出生点就在第一列。）
4. 你要把所有 $S$ 块砖都摆进去，不多不少。

Creator 不会为难你，因此一定有一种关卡符合上述所有规则。

为了输出方便，你只需要给出第 $i$ 列有多少砖块（记为 $a_i$），输出 $a$ 序列即可。容易证明，一个合法的 $a$ 序列和一个合法关卡是一一对应的。

输入格式

仅一行 $4$ 个非负整数 $n,m,k,S$。

输出格式

输出一行 $n$ 个非负整数表示你构造的序列 $a$。如果有多种可能的序列，输出任意一个符合题意的序列即可。保证至少有一个序列满足题目要求。

4 6 2 11

2 4 2 3

3 4 5 6

4 2 0

提示

【数据范围】

该题共有 $10$ 个测试点，每个测试点等分。

• 对于 $20\%$ 的数据，$S=n\cdot m$。
• 对于 $20\%$ 的数据，$k=0$。
• 对于 $20\%$ 的数据，$k=10^9$。

对于 $100\%$ 的数据，$1\leqslant n,m\leqslant 10^5$，$0\leqslant k\leqslant 10^9$，$0\leqslant S\leqslant n\cdot m$。

【提示】

古之有数，其名为 $S$。$S$ 之大，一个 int （可能）装不下。

【样例解释 #1】

样例输出对应关卡如下。

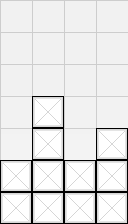
注意可能有多种合法关卡均符合条件。