题目描述

令满足如下条件的儿子有序的无标号有根树数量为 $w_k(n)$：

• 点数 $n_0\in[1,n]$。
• 所有深度为 $k$ 的点都不是叶子。

给定固定正整数 $k$，多次给定正整数 $n$，求 $w_k(n)\bmod 998244353$ 的值。

此处一个点的深度定义为它到根的唯一简单路径的长度，比如根的深度就是 $0$。

输入格式

本题有多组询问。

第一行一个正整数 $id$ 表示 Subtask 编号。

第二行两个正整数 $q,k$，其中 $q$ 表示询问次数。

后 $q$ 行，每行一个正整数 $n$，描述一组询问。

输出格式

$q$ 行，每行对应一个 $w_k(n)\bmod 998244353$。

0
5 2
1
2
3
4
5

1
2
3
5
10

0
5 200
1
10
100
1000
10000

1
6918
721868074
972431902
815282281

提示

样例解释

样例 1 解释：

$k=2$，树上恰有 $5$ 个点时的所有方案：

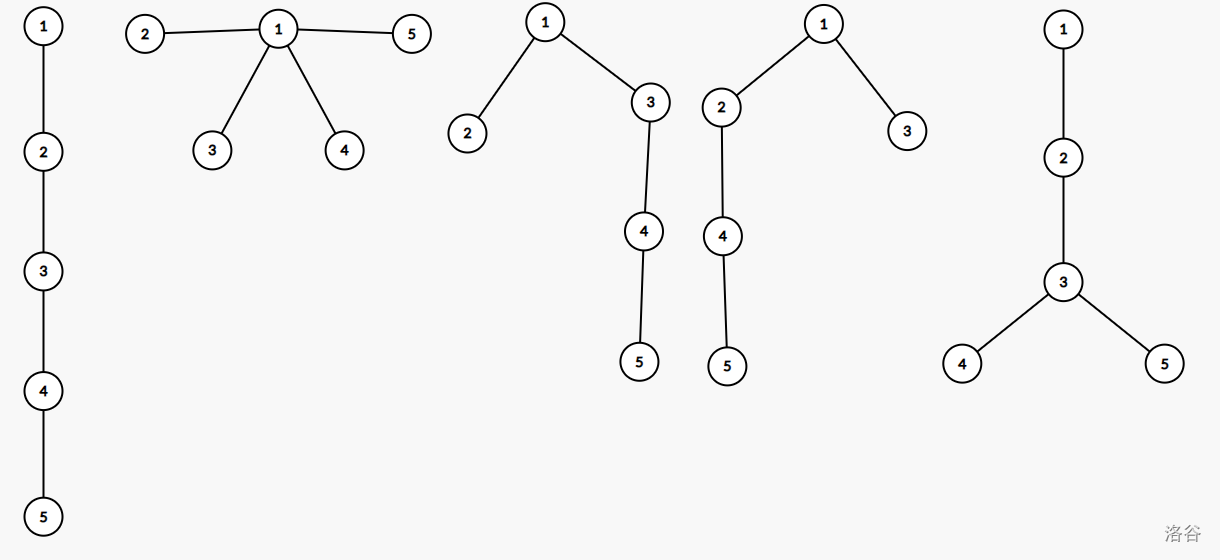
数据范围

本题采用捆绑测试。

$$\newcommand{\arraystretch}{1.5} \begin{array}{c|c|c|c}\hline\hline \textbf{Subtask} & \bm{n}\le & \textbf{分值} & \textbf{特殊性质}\\\hline \textsf{1} & 5 & 5 \\\hline \textsf{2} & 10^2 & 20\\\hline \textsf{3} & 2\times10^5 & 35 & k=1\\\hline \textsf{4} & 2\times10^5 & 40\\\hline\hline \end{array} $$

对于全部数据，$1\le n,q,k\le 2\times10^5$。