题目背景

张则雨和穆制程坐在天台上看着满天的星辰。在他们的世界，流行一种连接星星的活动。他们对此有一种浪漫的诠释：如果连不完，剩下的一颗星星就是身旁的人；如果连得完，那身边的人和自己都是星星。

题目描述

星空中有 $n$ 颗星星，第 $i$ 颗位于坐标 $(x_i,y_i)$。你需要把星星连接成满足张则雨的如下需求：

• 每一颗星星都是且仅是一条线段的端点，所有线段互不相交（包括端点）。
• 所有线段左右端点 $|x_l-x_r|$ 之和有最小值。

然而张则雨有点笨，并不知道应该怎么连。穆制程知道你是地球上最聪明的人，于是告诉你 $n$ 颗星星的坐标，你需要输出连接方案或者报告无解。

输入格式

第一行 $n$ 表示星星的数量。

从第二行开始，共 $n$ 行，每行两个整数。第 $i+1$ 行表示第 $i$ 颗星星的 $(x_i,y_i)$ 坐标。

输出格式

第一行输出所有线段左右端点 $|x_l-x_r|$ 的和的最小值。

接下来每一行输出两个编号，表示为了得到最小值，你每条线段连接的星星的编号。

如果有多种可能的连接方案，输出任意一种。如果无解在第一行输出 $-1$。

4
1 3
2 2
2 1
3 4

2
1 4
2 3

6
1 5
2 3
2 4
2 5
2 -1
3 -3

2
1 3
4 6
2 5

提示

样例 1 的方案如图：

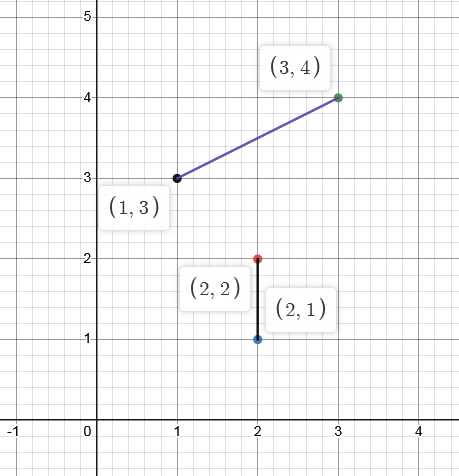
样例 2 的方案如图：

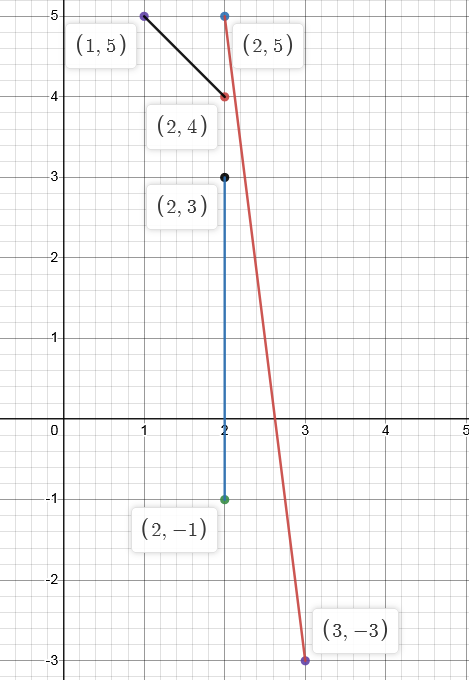
本题使用捆绑测试与子任务依赖。

特殊性质 $A$：满足所有 $x_i$ 都相等。

保证对于 $100\%$ 的数据，$1\leqslant n\leqslant5\times 10^5$，$0\leqslant|x|,|y|\leqslant 10^9$ 且对于任意 $i\ne j$，有 $(x_i,y_i)\neq (x_j,y_j)$。