题目背景

与其编写苍白无力的背景，不如出更有质量的题。

题目描述

我们称简单有向图 $G,H$ 本质相同，当且仅当：

• 对于任意点对 $(u,v)$，若在图 $G$ 中从 $u$ 出发能走到 $v$，则在图 $H$ 中从 $u$ 出发能走到 $v$。反之若在图 $H$ 中从 $u$ 出发能走到 $v$，则在图 $G$ 中从 $u$ 出发也能走到 $v$。

若对于简单有向图 $G$，不存在其他简单有向图 $H$ 与其本质相同，则我们称图 $G$ 为 单图。

$T$ 次询问，每次询问给定一个正整数 $n$，请你回答 $n$ 个点的有标号单图数。

输入格式

本题采用多组输入。

第一行输入两个整数 $T,mod$，表示数据组数与模数。

接下来 $T$ 行每行一个整数，表示这组数据的 $n$。

输出格式

输出 $T$ 行，第 $i$ 行表示第 $i$ 组数据的答案对 $mod$ 取模的值。

5 998244353
1
3
5
12
888

1
16
986
328006912
535268381

提示

数据范围

「本题采用捆绑测试」

• $\operatorname{Subtask} 1(30\%)$：$T = 1$，$n \leq 5$。

• $\operatorname{Subtask} 2(50\%)$：$T \leq 10$。

• $\operatorname{Subtask} 3(20\%)$：无特殊限制。

对于 $100\%$ 的数据满足：$1 \leq T,n \leq 1000$，$1\leq mod \leq 10^9$。

说明提示

这里给出一些例子来帮助理解单图的含义：

---

这是一张单图，可以证明不存在其他图与其本质相同。

---

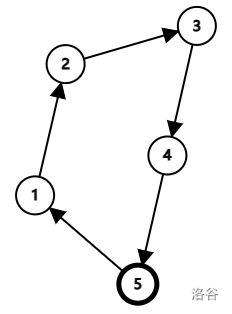
这不是一张单图，因为我们可以添加边 $(5,2)$ 构造出与其本质相同的图。

---

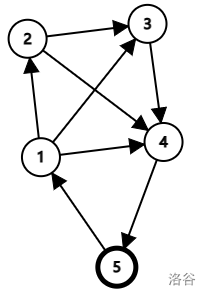
这不是一张单图，因为我们可以删去边 $(1,3)$ 构造出与其本质相同的图。