#P9224. 「PEOI Rd1」k 叉堆(heap)
「PEOI Rd1」k 叉堆(heap)
Description
给定一个 的序列,每个位置 有 个参数 。已知这个序列是一个按照大根堆的 bfs 序得到的序列。
bfs 序,即按照下图中红色数字编号的顺序:
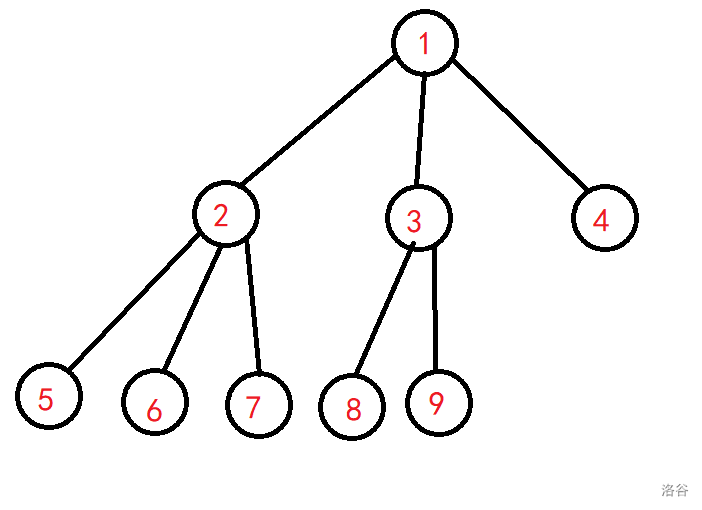
一个大根堆满足条件,当且仅当所有子节点的所有 个权值都小于等于父节点,即 $\forall u\in[1,n],\forall v\in son(u),\forall j \in [1,k],a_{v,j} \leq a_{u,j}$。
假设这个大根堆是完全 叉树,求所有 ,使得这个 叉堆满足条件的 的取值。
Input Format
第一行两个整数 。
接下来 行,每行 个整数,表示给定的序列。其中,第 行第 列表示的是 。
可以理解为,分成 行给出了所有位置的 个参数。
Output Format
第一行一个整数 ,表示所有可能的 的取值数量。
接下来一行 个整数,表示所有的可能的 的取值。
3 2
1 1 1
1 1 1
2
1 2
6 1
2 1 2 1 1 2
2
2 5
Hint
样例解释
样例 中, 叉堆显然都符合条件。
数据范围
| 子任务编号 | 分值 | |
|---|---|---|
对于 的数据,保证 ,,。

 京公网安备 11011102002149号
京公网安备 11011102002149号