#P9221. 「TAOI-1」Pentiment
「TAOI-1」Pentiment
Description
我们规定,在 行 列的网格中,“直角蛇”是这样一条路径:
- 从最下方(第一行)的某个格子的中心开始,在最上方(第 行)的某个格子的中心结束。
- 每次可以向上、向右或向左移动一格,每次移动后都到达某个格子的中心(不能向下移动)。
- 不能重复经过同一个格子。
特别地,为了给你增加一些考验,我们规定有一些格子是“直角蛇”不能经过的。
请你统计在给定的网格中存在多少种这样的“直角蛇”。答案对 取模。
Input Format
第一行三个整数 ,代表网格的行数和列数,以及限制的数量。
接下来的 行,每行两个整数 ,代表第 行第 列的格子不能经过。保证同一个格子至多出现一次。保证所有格子按照 为第一关键字, 为第二关键字,从小到大排序后给出。(我们规定最下方的格子的行数为 ,最左侧格子的列数为 )
Output Format
共一行一个整数,代表符合条件的“直角蛇”数量对 取模的结果。
2 3 2
1 1
2 1
8
4 4 4
1 1
2 2
3 3
4 4
0
6 5 4
1 3
3 1
3 4
5 2
2000
100000000 100000000 0
103866487
Hint
数据范围
本题采用捆绑测试。
- Subtask 1(10 points):,。
- Subtask 2(10 points):。
- Subtask 3(15 points):。
- Subtask 4(20 points):。
- Subtask 5(20 points):。
- Subtask 6(25 points):无特殊限制。
对于所有测试数据,,,,,。
样例解释
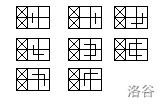
如图,样例一中共有八种满足条件的“直角蛇”。
对于样例二,不存在满足条件的“直角蛇”。
在寂若死灰中屈服。
在飘忽不定中屈服。
在功亏一篑中屈服。

 京公网安备 11011102002149号
京公网安备 11011102002149号