题目背景

不死鸟之尾，一种量产型的羽毛。可用作药品。

虽说是量产型，可是从哪里可以得到这种万能之药呢？

题目描述

有一个包含 $n$ 个停车位的停车场，里面的停车位排成了一排，最左边和最右边都是墙壁。

有 $n$ 辆车要按顺序依次停入这个停车场，在停入第 $i$ 辆车时，这辆车要停入的位置左右两边的空位越多，停进去需要的时间也就会越少，具体地，如果其左边连续的空位数量为 $l$，其右边连续的空位数量为 $r$，那么停入该辆车所需时间为 $W_i-L_i\cdot l-R_i\cdot r$，其中 $W_i,L_i,R_i$ 会给出（特别的，停车所需要的时间不会是负数，所以我们保证 $W_i\ge L_i\cdot n+R_i\cdot n$）。

对于连续空位的解释：例如，下图中箭头所指位置左边连续空位为 $1$，右边连续空位为 $2$。

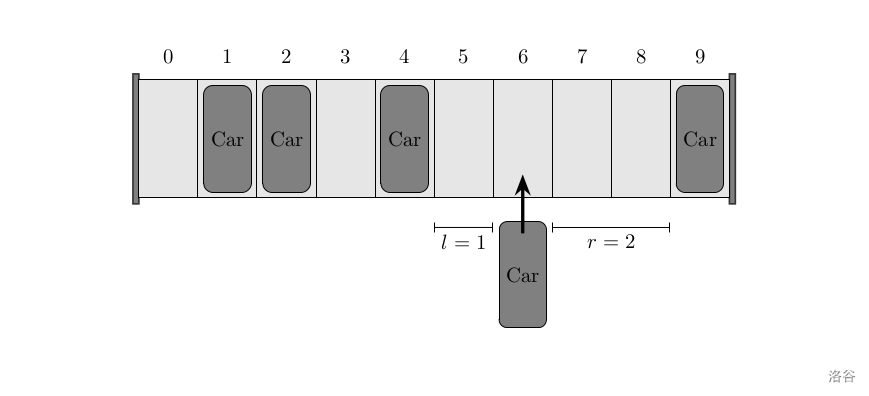
请依次确定每一辆车停入的位置，使得停入所有车所需时间最小。

输入格式

输入第一行一个整数 $n$。

接下来三行，每行 $n$ 个整数：第一行第 $i$ 个数给出 $W_i$，第二行第 $i$ 个数给出 $L_i$，第三行第 $i$ 个数给出 $R_i$。保证 $W_i\ge L_i\cdot n+R_i\cdot n$，$L_i,R_i\ge 0$。

输出格式

输出一个数表示所需要的最少时间。

3
18 20 22
1 2 3
1 4 3

54

提示

样例解释 1

第 $1$ 辆车停入从左往右数第 $3$ 个停车位，此时该停车位左边有 $2$ 个连续空位，右边没有连续空位，所需时间 $18-1\times 2-1\times 0=16$。

第 $2$ 辆车停入从左往右数第 $1$ 个停车位，此时该停车位左边没有连续空位，右边有 $1$ 个连续空位，所需时间 $20-2\times 0-4\times 1=16$。

第 $3$ 辆车停入从左往右数第 $2$ 个停车位，此时该停车位左右都没有连续空位，所需时间 $22-3\times 0-3\times 0=22$。

停入所有车需要时间 $16+16+22=54$。

数据范围

对于所有数据，保证 $1\le n\le 10^5$，$0\le L_i,R_i\le 10^5$，$nL_i+nR_i\le W_i\le 2\times 10^{10}$。