题目背景

徐福是秦朝齐地方士。

奉秦皇之命，徐福率三千童男童女踏上了寻找传说中的「蓬莱之药」的征途。但最后再也没有回来。

徐福最终去了哪里？有没有找到蓬莱之药？这些问题已经无关紧要了。

题目描述

时间的流逝可以抽象成对数字序列进行排序所花费的时间。不同排序策略花费的时间是不同的。这里介绍一种人类探索排序过程中具有里程碑意义的一种排序算法：希尔排序。

希尔排序可以被视为一种对插入排序的优化。为了研究希尔排序的运行效率，我们希望你实现一个简单的希尔排序的过程。在这之前，我们会规范插入排序的具体流程以及评价一个插入排序的过程的「代价」。

插入排序

对于一个长度为 $n$ 的数组 $a=[a_1,a_2,\cdots,a_n]$，插入排序的思想是，从前到后枚举每一个元素，将其插入到正确的位置上去：

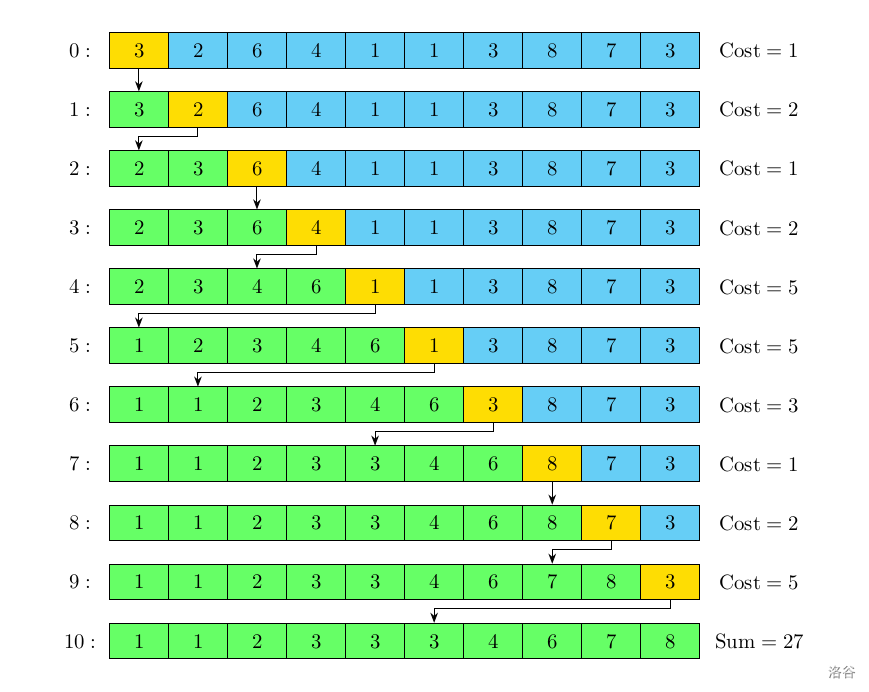
如图所示是一个典型的插入排序的过程。在第 $i$ 轮中我们把下标为 $i$ 的元素插入到了排好序的部分中第一个比 $\bm{a_i}$ 大的元素之前。假设 $a_i$ 最终被插入到了 $b_i$ 位置，那么我们称这一轮的代价为 $|a_i-b_i|+1$，整个插入排序的过程的代价就是每一轮的代价之和。

希尔排序

为了减小插入排序的代价，我们引入了希尔排序。希尔排序将整个排序过程分成了若干轮，每一轮会按照一定的间隔把元素分组，对每一组内的元素分别进行排序。在最后一轮，希尔排序会对整个数组进行一次最终的插入排序。

具体的分组方式是，选定一个整数 $d$，划分为如下组别：

• 下标为 $1,1+d,1+2d,\cdots$ 的元素；
• 下标为 $2,2+d,2+2d,\cdots$ 的元素；
• 下标为 $3,3+d,3+2d,\cdots$ 的元素；
• ……
• 下标为 $d,2d,3d,\cdots$ 的元素。

下面是一轮希尔排序的过程。我们选定 $d=3$。

希尔排序每一轮分别选取 $d$，并且在最后一轮取 $d=1$，每一轮都进行这样的排序，最终得到一个有序的数组。

虽然看上去进行了很多轮插入排序，但是最终每一轮插入排序的代价之和可能会远小于对整个数组进行单次插入排序的代价（上述例子中体现得并不明显，可以参考样例 $2,3$ 给出的例子）。

事实上，希尔排序是人类发现的第一个最坏复杂度低于 $\Theta (n^2)$ 的排序算法。例如，当取 $d=2^k-1,\ k=\lfloor\log_2 n\rfloor,\lfloor\log_2 n\rfloor-1,\lfloor\log_2 n\rfloor-2,\cdots,1$ 时，整个过程的最坏时间复杂度为 $\mathcal \Theta(n^{3/2})$。

输入格式

第一行有两个整数 $n,m$，分别表示待排序的数组的长度以及希尔排序进行的轮数。

第二行有 $n$ 个整数 $a_1,a_2,\cdots,a_n$，描述数组里的元素。

第三行有 $m$ 个整数 $d_1,d_2,\cdots,d_m$，描述每一轮选取的 $d$ 的值。数据保证 $d_m=1$。

输出格式

第一行输出一个整数 $\mathrm{cost}$，表示整个希尔排序过程中插入排序产生的代价之和。

第二行输出 $n$ 个整数，表示数组 $a$ 排序后的结果。

10 1
3 2 6 4 1 1 3 8 7 3
1

27
1 1 2 3 3 3 4 6 7 8 

15 1
15 14 13 12 10 11 9 8 7 4 5 6 3 2 1
1

116
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

15 3
15 14 13 12 10 11 9 8 7 4 5 6 3 2 1      
9 3 1

68
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

提示

数据范围及约定

对于全部数据，保证 $1\le n\le 10^5$，$1\le m\le 100$，$\mathrm{cost}\le 5\times 10^7$，$1\le a_i\le 10^9$，$1\le d_i\le n$，$d_m=1$。