#P9150. 邮箱题
邮箱题
Description
有一张 个点和 条边构成的有向图。每个点内都有一把另一个点的钥匙, 号点内有 号点的钥匙。你能进入一个点当且仅当你有该点的钥匙。保证 构成排列。
只要进入了一个点,就获得了这个点内有的钥匙。一旦获得钥匙就不会被消耗。
现在你拿到了 号点的钥匙并到了 号点。你需要对每个 求出:
- 有多少点能被你到达。
- 有多少点能被你到达并返回起点 。
请注意:给出的边均是有向边!
Input Format
本题有多组数据。
第一行,一个正整数 ,表示数据的组数。对于每组数据:
第一行,两个整数 ,表示图的点数和边数。
第二行, 个整数 ,表示 号点内有 号点的钥匙。保证 构成排列。
接下来 行,每行两个整数 ,表示图上的一条从 指向 的有向边。保证不含重边或自环。
Output Format
对于每组数据,输出 行,每行两个整数,第 行的整数分别表示从 号点出发,能到达的点数和能到达并返回起点的点数。
3
4 5
2 3 4 1
1 2
2 3
3 1
1 4
4 3
5 6
2 3 4 5 1
1 2
2 3
3 4
4 5
5 2
4 1
3 2
2 3 1
1 2
1 3
4 4
2 1
1 1
1 1
5 5
5 5
3 1
2 1
1 1
2 1
1 1
1 1
Hint
【样例解释】
以下是第一组数据的解释:(图中括号内的内容为点上的钥匙编号)
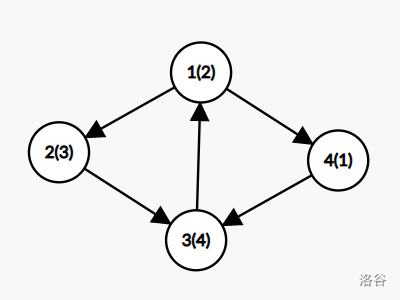
- 能到达的结点集合为 , 能到达且能返回 的结点集合为 ;
- 能到达的结点集合为 , 能到达且能返回 的结点集合为 ;
- 能到达的结点集合为 , 能到达且能返回 的结点集合为 ;
- 能到达的结点集合为 , 能到达且能返回 的结点集合为 。
这是一个合法的遍历过程:从 开始,初始钥匙为 ,到达结点 并获得钥匙 ,到达结点 并获得钥匙 ,回到结点 ,到达结点 并获得钥匙 ,到达结点 ,回到结点 。
【数据范围】
对于 的数据,满足 ,,,,,,保证图中不含重边或自环。
本题采用捆绑测试且开启子任务依赖!
| 子任务 | 对 的约束 | 对 的约束 | 分值 | 依赖 |
|---|---|---|---|---|
| 1 | \ | |||
| 2 | ||||
| 3 | 子任务 1、2 | |||
| 4 | 子任务 1、2、3 | |||

 京公网安备 11011102002149号
京公网安备 11011102002149号