题目描述

题目译自 PA 2020 Runda 5 Królewski bal

自古以来，Byteotia 的所有统治者都会举行奢华的舞会，Byteur 国王也不例外。然而，每当他组织一次，他就觉得少了点什么。因此，他决定在下一次舞会中加入一些艺术元素。

为此，Byteur 国王委托他的首席顾问编排演出，不久之后，首席顾问向他提出了自己的设想。

根据顾问的计划，$n^2$ 名马戏团演员将参加演出，其中 $n$ 是一个正整数。在演出的压轴部分，他们将排成 $n$ 行，每行恰好有 $n$ 个马戏团演员，从而形成一个 $n\times n$ 大小的正方形。在压轴部分开始时，每个演员将带或不带燃烧的呼拉圈跳舞。在午夜时分，一些带着呼啦圈跳舞的马戏团演员可能会把呼啦圈扔给其他没有带呼啦圈跳舞的马戏团演员。每个演员最多允许扔给一个其他的演员。

他们都会在同一时间进行投掷。他们是专业人士，所以他们的呼啦圈肯定不会在空中相撞，但这里有一个问题。每次投掷必须在位于同一行或同一列的演员之间进行。

值得一提的是，Byteur 国王喜欢大规模的行动，所以马戏团演员的数量可能非常庞大。在制定计划时，他的顾问首先确定了数字 $n$，并假设所有马戏团的演员都会在没有燃烧呼拉圈的情况下开始最后的表演。然后，他会选择 $m$ 次一些特定的行列范围，画出一个矩形，并使得这个区域中的每个演员应该以不同的方式开始压轴表演。即，如果在之前的方案中他们拿着呼啦圈开始，则这版方案中他们就不拿呼啦圈开始，反之亦然。

Byteur 国王在得知顾问的计划后，立即明白，为了使演出尽可能地壮观，呼啦圈的抛掷次数应该尽可能地多。Byteur 国王想知道这个数字，但这并不容易，因为他不断修改计划。他的每项修改（他总共已经做了 $q$ 次修改）都涉及到挑选一个马戏团演员并改变他开始压轴表演的方式（即如果他之前拿着呼啦圈开始，那么他现在就不拿着呼啦圈开始，反之亦然）。国王的修改在方案上永久保留，也就是说，如果有任何适用于某个马戏团演员的修改，这个修改的效果一直保留到最后，除非国王再次修改他。

因此，顾问的任务并不简单。帮助他，对于区间 $[0, q]$ 中的每个整数 $i$，在考虑国王的前 $i$ 次修改后，确定可能发生的最大投掷次数。

输入格式

第一行三个整数 $n,m,q$。

接下来 $m$ 行描述顾问的方案，每行包含四个整数 $x_1,y_1,x_2,y_2$，表示对行编号 $x_1$ 到 $x_2$（包含两端），列编号 $y_1$ 到 $y_2$（包含两端）的艺术家进行一次操作。行列编号均从 $1$ 到 $n$。

接下来 $q$ 行描述国王的修改，第 $i$ 行包含两个数 $a_i,b_i$，表示国王修改第 $a_i$ 行第 $b_i$ 列的演员状态。

输出格式

输出 $q+1$ 行，第 $i$ 行输出如果考虑国王的前 $i-1$ 次修改，可能发生的最大投掷次数。

4 3 4
1 2 4 2
3 1 3 4
3 2 3 2
4 4
3 2
4 3
4 4

6
7
7
8
7

7 2 0
1 1 6 6
2 2 7 7

22

提示

样例 1 解释

下图展示了国王进行了第一次修改后的情况。演出开始有呼啦圈的演员用加粗圆圈标出，箭头标明了可能发生的投掷。

---

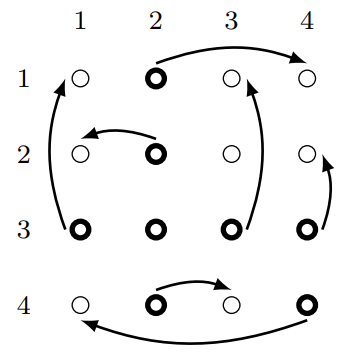
数据范围

本题采用捆绑测试

• 对于一些子任务，满足 $n\le 50$，$m\le 10^4$，$q=0$。
• 对于一些其他的子任务，满足 $n\le 200$，$m\le 10^5$，$q\le 10$。
• 对于一些其他的子任务，满足 $n\le 2\times 10^3$，$m\le 10^5$，$q\le 5\times 10^3$。
• 对于一些其他的子任务，满足 $q=0$。

对于上述情况，至少有一个子任务满足。

对于 $100\%$ 的数据，保证 $1\le n\le 3\times 10^5$，$0\le m,q\le 3\times 10^5$，$1\le x_1\le x_2\le n$，$1\le y_1\le y_2\le n$，$1\le a_i,b_i\le n$。

此外，对于每个子任务，至少满足以下条件中的一个：

• $n\le 2\times 10^3$
• 时间限制为 $12$ 秒

由于未给出具体子任务时间限制，因此在洛谷上所有子任务的时间限制均为 $3$ 秒。