题目描述

题目译自 PA 2020 Runda 5 Bardzo skomplikowany test

Bytie 刚刚参加了算法和数据结构这门课的面试。他没有为之学习太长时间，所以他做得不是太好。经过几分钟的交谈，这位心碎的主讲老师决定给这个男孩最后一次机会。

• 「孩儿，你知道啥是 BST 不？」教授问

Bytie 听到这句话后内心狂喜，因为在他上课睡觉的时候记住了一些理论。

• 「知道。大小为 $n$ 的 BST 是一棵有根树，其顶点用 $1$ 到 $n$ 的整数来编号。每个节点最多可以有两个子节点；它可以有一个最多一个左子节点和一个最多一个右子节点。此外，每个节点的编号必须大于其左子树中所有节点的编号，并小于其右子树中所有顶点的编号。」Bytie 回答说，他达到了他潜意识的深处。
• 「很好。让我们看看你是否记住了如何对 BST 进行旋转。」一直坐在那里的教授回答说。他站起来，向黑板走去。

Bytie 被冷汗浸透了。他一时失去了信心，因为他记不起旋转的具体原理（可能在上这节课的时候，他正在另一边摸鱼，没听课）。考官在黑板上画了两棵同样大小的 BST 树，并让 Bytie 用正确的旋转将第一棵树转化为第二棵树。

Bytie 想了一会儿，认为左旋就是选择某个节点 $v$ 和它的右子节点 $w$，并让 $w$ 成为 $v$ 的父节点。Bytie 的直觉用以下伪代码描述。

if v.Parent != null then
    if v.Parent.RightSon == v then
        v.Parent.RightSon := w
    else
        v.Parent.LeftSon := w
w.Parent := v.Parent
v.Parent := w
w.LeftSon := v
v.RightSon := null

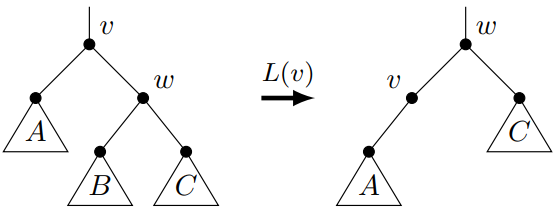
以此类推，Bytie 理解了右旋，其中 $w$ 是 $v$ 的左子节点。

if v.Parent != null then
    if v.Parent.RightSon == v then
        v.Parent.RightSon := w
    else
        v.Parent.LeftSon := w
w.Parent := v.Parent
v.Parent := w
w.RightSon := v
v.LeftSon := null

然而，Bytie 很快就注意到有些不对劲。如果节点 $w$ 在左旋时有左子树，它就会丢失！同样在右转过程中，节点 $w$ 的右子树也会丢失。

• 「快点孩儿，你不是唯一一个想通过这次考试的人。」教授不耐烦地催促道。

在没有太多时间考虑的情况下，Bytie 假设只有在这个有问题的子树是空的情况下才能执行旋转，也就是说，如果没有顶点丢失并且树保持一致的话才进行旋转。

为了尽快结束他的煎熬，他决定进行最少次数的旋转，使他能够将第一棵树变成第二棵。请告诉他这是否可行，如果可行，他需要进行多少次轮换？由于这个数字可能相当大，请告诉他这个值对 $10^9+7$ 取模后的值。

输入格式

第一行包含一个整数 $n$，表示这个 BST 的大小。

接下来两行描述这两棵树。对于一棵树用一行 $n$ 个整数 $a_1,a_2,\cdots,a_n$ 描述。如果 $a_i\ge 1$，表示 $i$ 节点的父节点；如果 $a_i=-1$，则表示这是树的根节点。

你可以假设这两棵树都是合法的 BST，即树中没有环，恰好有一个根节点，每个节点最多只有一个比自己小的子节点和一个比自己大的子节点。

输出格式

输出应该包含一个整数，表示用 Bytie 的方式把第一棵树转化为第二棵树所需最少旋转次数对 $10^9+7$ 取模后的值，如果不可能转化，输出 $-1$。

4
3 1 -1 3
2 -1 4 2

3

8
2 4 2 7 4 5 -1 7
2 3 6 5 3 -1 6 7

7

提示

样例 1 解释

下图展示了旋转最小次数所采取的旋转方式。

---

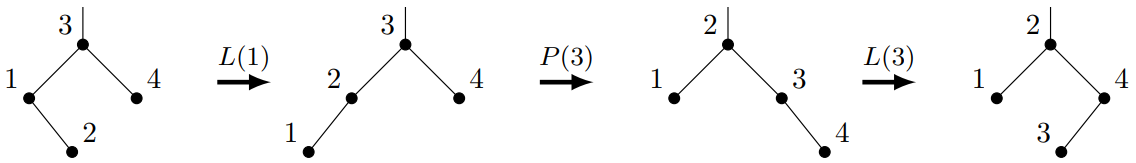
数据范围

本题采用捆绑测试

对于 $100\%$ 的数据，保证 $1\le n\le 5\times 10^5$，$-1\le a_i\le n$，$a_i\neq 0$。