#P9083. [PA 2018] Ryki
[PA 2018] Ryki
Description
Berlandia 是一个由方格组成的无限大棋盘。行从下到上用递增的整数编号,列从左到右用递增的整数编号。令 表示第 行第 列的方格。如果两个不同方格至少有一个角接触,我们就称这两个格子相邻。这意味着格子是八连通的。
两个格子 与 之间的距离是欧几里得距离,也就是:
Berlandia 地区居住着 只熊。第 只熊居住在方格 处。同一方格中可以居住多只熊。
熊可以单独生活,但是有时也会相互靠近。当一只熊吼叫时,其他方格中所有的熊会立即移动到相邻的方格中离吼叫的熊最近的方格。可以证明有且仅有一个这样的方格(不会出现并列情况)。与吼叫的熊在同一方格的熊不会移动位置。
例如,考虑一对熊,一只在方格 ,另一只在方格 。方格 中的熊吼叫会让另一只熊移向方格 ,这两只熊最后相距 。
这些熊会按第一只,第二只,……,最后一只的顺序依次吼叫。除了一只叫 Limak 的熊,他太冷了以至于吼不出来,并且他也不能离开他所在的方格,可怜的 Limak。
但你不知道 Limak 是哪只熊,对于 到 的每一个 ,如果第 只熊是 Limak,请找出所有熊的最终位置。对于每种可能,输出所有熊的横纵坐标乘积之和就可以了。也就是说,假设在 次吼叫后,第 只熊在 ,则输出:
Input Format
输入第一行包括一个正整数 ,表示熊的数量。
接下来 行,每行两个整数 ,第 行表示第 只熊的初始位置。
Output Format
输出 行,第 行输出一个整数,表示假设 Limak 是第 只熊的话,最终所有熊所在行列之积的和。
4
3 5
2 1
1 4
2 1
27
24
25
35
Hint
样例 1 解释
下图展示了 的情况,即熊的吼叫顺序为 。红色圆圈表示吼叫的熊。最后乘积的和为 。
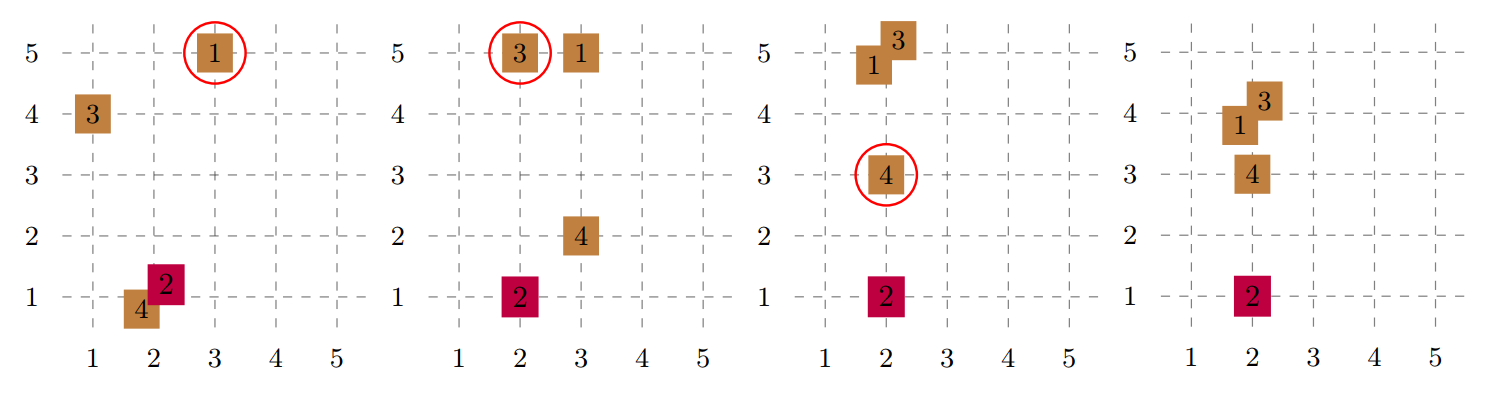
数据范围
本题采用捆绑测试
保证每组子任务中下述三种情况至少出现一种:
- 对于所有 都有
- 时间限制为 秒
注:由于未公布每个测试点的详细时间限制,因此本题所有测试点的时间限制均为 秒。

 京公网安备 11011102002149号
京公网安备 11011102002149号