#P9036. 「KDOI-04」挑战 NPC Ⅲ
「KDOI-04」挑战 NPC Ⅲ
Description
小 S 有一个伟大的梦想:证明 。
有一天,他得知一般图最大独立集是 NPC 问题后,决定解决他。
当然小 S 太菜了,解决不了,于是求助于你:
给出一个含有 个顶点, 条边的无向图 ,求 中大小恰好为 的独立集的数量。由于答案可能很大,请将其对 取模。
小 S 不喜欢多测,因为他在 NOIp 中因为多测挂分,所以本题包含多组测试数据。
Input Format
本题包含多组测试数据。
第一行一个正整数 ,表示测试数据组数。
对于每组测试数据,第一行三个正整数 。
接下来 行,每行两个正整数 表示一条边。
保证图中不存在自环,但可能存在重边。
Output Format
对于每组测试数据,输出一行一个正整数,表示符合要求的独立集数量。答案对 取模。
3
4 6 1
1 2
1 3
1 4
2 3
2 4
3 4
4 6 3
1 2
1 3
1 4
2 3
2 4
3 4
8 13 5
1 2
7 8
1 3
2 5
3 8
6 8
4 7
5 6
5 7
5 8
6 7
1 8
3 5
0
4
8
Hint
【样例解释】
对于第 组测试数据,图是完全图,容易发现,完全图的最大独立集为 ,并且每一个顶点都单独构成一个独立集。因此第 组测试数据的答案为 ,第 组测试数据的答案为 。
对于第 组测试数据,该组数据中给出的无向图如下:
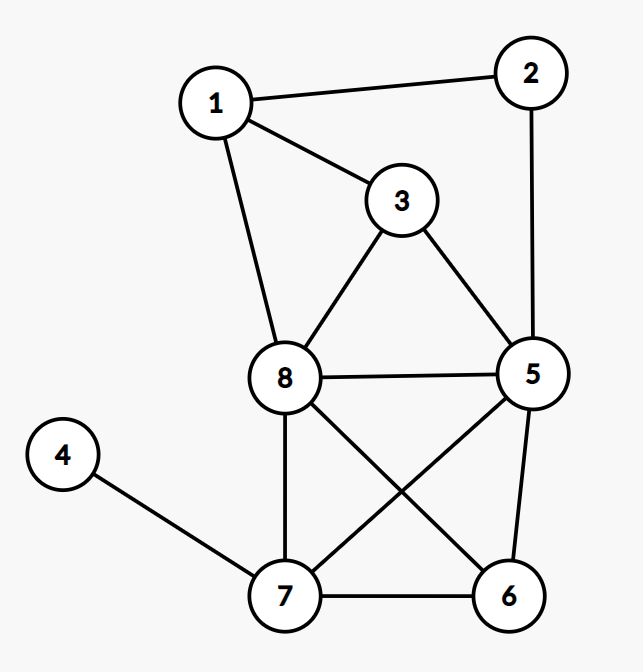
其中,所有大小为 的独立集为:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- 。
【数据范围】
本题采用捆绑测试。
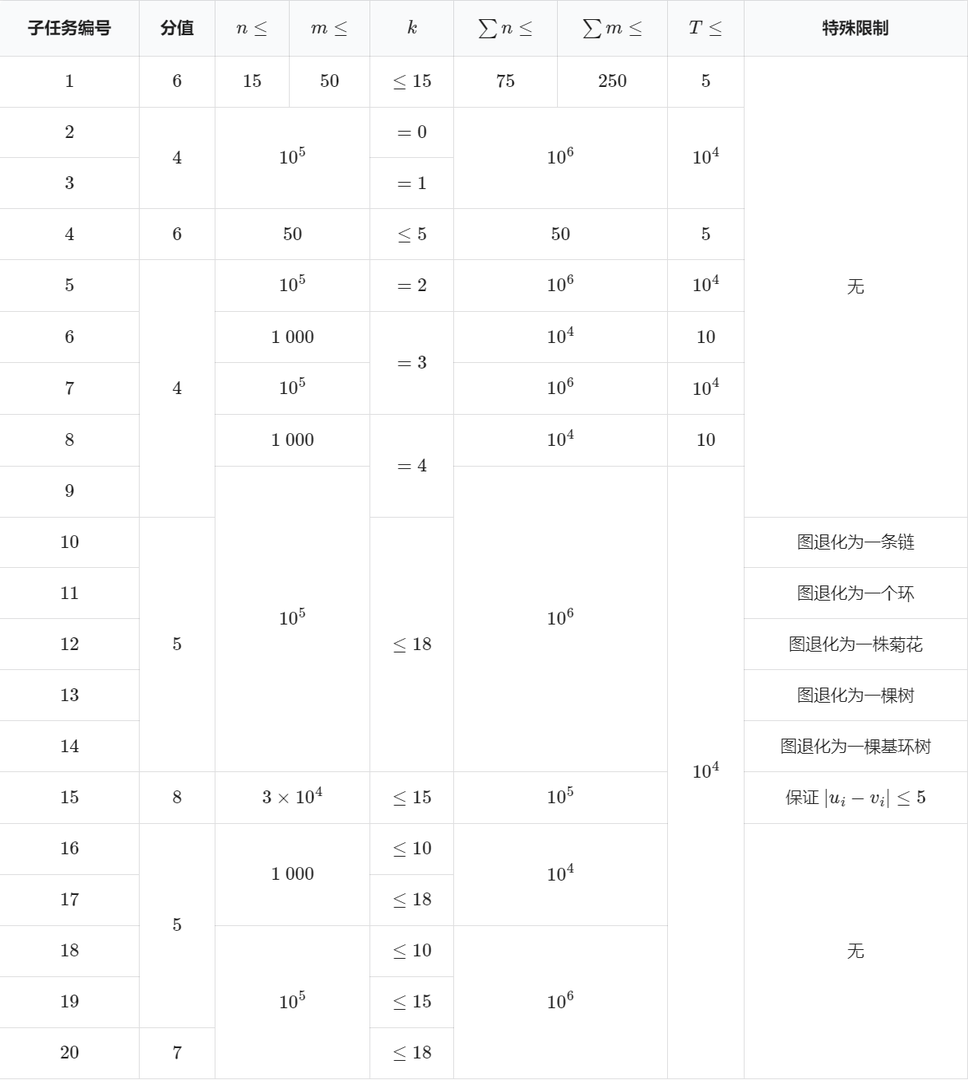
对于 的数据,保证 ,,,,。
并且对于每个测试点保证:
设 ,即该测试点中所有 的最大值,
- 若 ,则 ;
- 若 ,则 ;
- 若 ,则 ;
- 若 ,则 。

 京公网安备 11011102002149号
京公网安备 11011102002149号