题目描述

给定平面上的 $N$ 个点，和一棵大小为 $N$ 的树 $T$，保证这棵树上每个点的度数至多为 $3$，树上节点按 $1\sim N$ 编号。

你需要为平面上的点使用 $1\sim N$ 的编号重编号之后，对于所有树上的边 $e=(u,v)$，将平面上的点 $u$ 和平面上的点 $v$ 用线段连接后，任意两条线段除了在端点上相交没有其他的相交点。

试构造一组方案，保证一定有解。

输入格式

第一行一个整数 $N$。

接下来 $N-1$ 行，一行两个整数 $a,b$，表示有一条从 $a$ 连向 $b$ 的边。

接下来 $N$ 行，一行两个整数 $x,y$，表示一个点的横纵坐标为 $(x,y)$。保证这 $N$ 个点两两不同，且没有任意三点共线。

输出格式

输出一行 $N$ 个整数，第 $i$ 个数应为原本的第 $i$ 个点的标号。

3
1 2
2 3
10 10
10 20
20 10

1 2 3

5
1 2
1 3
1 4
4 5
10 10
10 30
30 10
30 30
20 25

5 4 2 3 1

6
1 2
2 3
1 4
4 5
4 6
10 60
10 40
40 50
40 30
70 30
70 10

6 5 4 1 2 3

提示

样例 3 解释

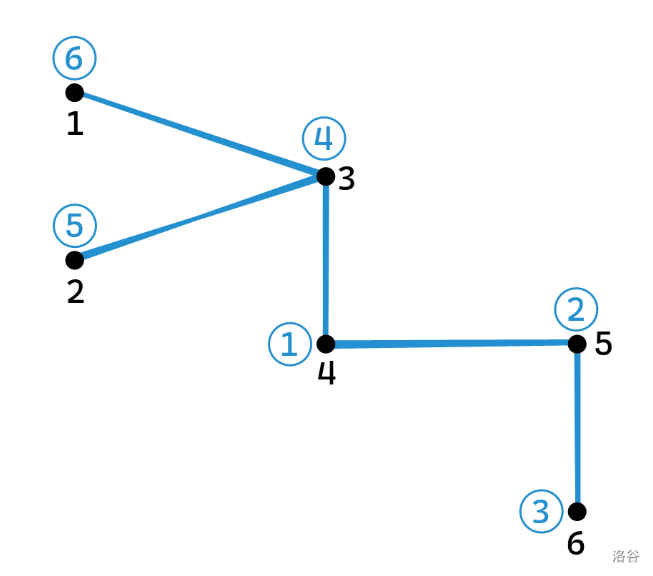
蓝色数字表示所分配的编号，黑色数字表示原本的编号。

数据规模与约定

对于所有数据，保证 $0\le x,y\le 10^9$。