题目描述
这是一道交互题。
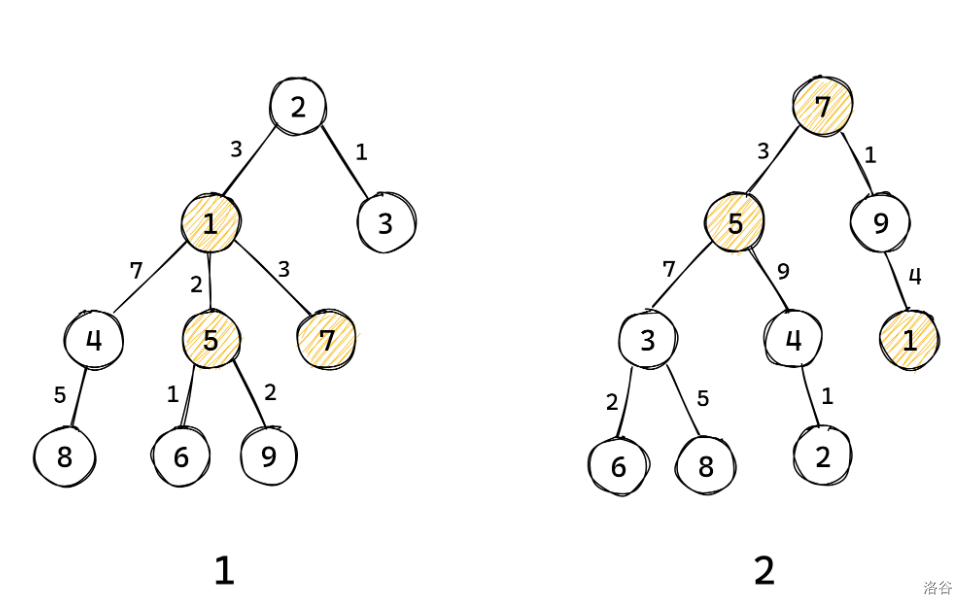
Tomislav 在睡梦中想到了一个问题:给定两棵大小为 N 的树,树上的节点按 1∼N 分别编号,树则分别编号为树 1,树 2,树有边权,但是边权被隐藏了起来。
Tomislav 需要向交互库提供一个大小为 K 的编号的子集 S,在选择了这个集合后,小 C 可以问 Q 个格式为 (a,b) 的问题,定义 dt(x,y) 表示树 t 上节点 x 与节点 y 的距离,lt 表示树 t 上节点 a 与节点 b 的 LCA,交互库会依次回答 d1(l1,a),d1(l1,b),d2(l2,a),d2(l2,b)。
紧接着交互库会询问 T 个格式为 (p,q) 的问题,其中 p,q∈S,Tomislav 必须依次回答 d1(p,q) 和 d2(p,q)。
可怜的 Tomislav 并不会做,请你帮帮他。
输入格式
第一行输入四个整数 N,K,Q,T。
接下来两行,每行 N 个整数,第一行描述树 1,第二行描述树 2。描述方式为,给出 N 个整数 p1,p2,…,pN,如果 pi 为 −1,则 i 为树的根,否则 pi 为 i 的父亲。
接下来请输出 K 个整数 x1,x2,…,xK 表示小 C 给出的编号集合 S,输出后请刷新缓冲区。
接下来你可以输出至多 Q 行,格式为「? a b」,表示询问 (a,b),当你的程序停止询问时,输出一行 「!」,表示结束询问,输出后请刷新缓冲区。
交互库会在你结束询问后返回所有询问的答案,分行返回,一行四个整数 d1(l1,a),d1(l1,b),d2(l2,a),d2(l2,b),表示询问的答案。
接下来输入 T 行,每行两个整数 p,q,表示一组交互库的询问。
你的程序需要回答这 T 个询问,具体的,对于每一个询问,你需要输出一行两个整数 d1(p,q) 和 d2(p,q),在你回答完所有的问题后,刷新缓冲区。
附加文件中会有一份示例程序,这份程序可以通过下面的样例,你可以根据这份程序理解交互过程。
提示
数据规模与约定
对于全部数据,保证所有边权为正整数且不超过 2000,2≤K≤105,1≤T≤min(K2,105)。
| Subtask 编号 |
特殊限制 |
分数 |
| 1 |
N=5×105,Q=K−1,树 1 与树 2 完全相同,包括边权 |
10 |
| 2 |
N=5×105,Q=2K−2 |
25 |
| 3 |
N=5×105,K=200,Q=K−1 |
19 |
| 4 |
N=106,K=103,Q=K−1 |
22 |
交互示例
| 示例输出 |
示例输入 |
|
9 3 2 3 |
2 -1 2 1 1 5 1 4 5 |
9 4 5 5 7 3 -1 3 7 |
1 5 7 |
|
? 1 5 |
? 1 7 |
! |
|
0 2 5 3 |
0 3 5 0 |
1 7 |
7 5 |
5 1 |
3 5 |
|
5 3 |
2 8 |


 京公网安备 11011102002149号
京公网安备 11011102002149号